A model of solute diffusion in unsaturated double-porosity medium by homogenization

Abstract

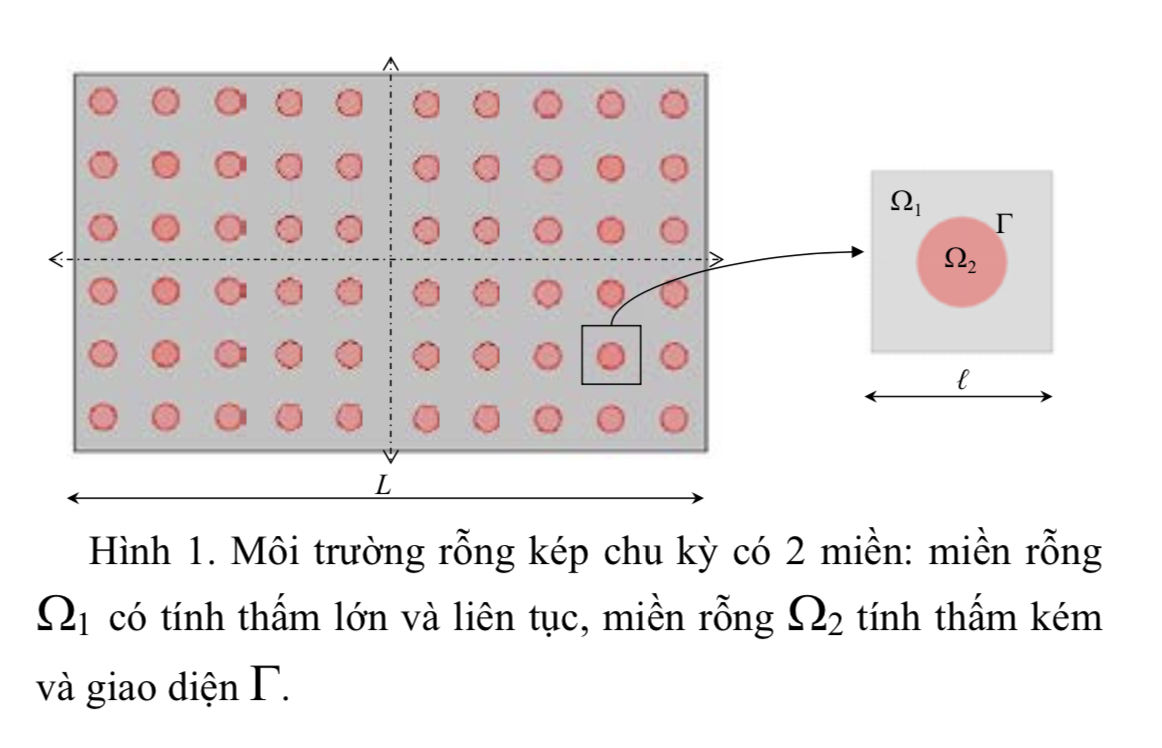
Solute diffusion is a key process in many fields like for example material science or environmental engineering. Diffusion mechanism in porous media is often described by Fick’s law. However, we could not use this law for nonstandard diffusion behaviors occurring in cases of heterogeneous media. The conception of double-porosity medium can be applied to a class of such media. The double-porosity medium is characterized by two distinct pore sizes: macro-porosity domain and micro-porosity domain, respectively, having the contrasted hydraulic properties. This paper presents the development of a macroscopic model for the solute diffusion in unsaturated double-porosity medium, by using homogenization method. The obtained macroscopic model is a system of two equations coupling on the interface of the macro- and micro-porosity domain for diffusion. This model contains the effective diffusion tensor representing for the entire medium. The developed model is verified by comparing with the reference solution of the fine scale model through a 3D numerical example of hydrogeology problem.