Open Access 
Abstract
Energy loss straggling was found to be critical in evaluating the energy reaction using heavy-ion beams during the early stage of experiments at accelerator facilities. Despite a significant attempt in simulating this quantity using computer codes such as LISE++ and SRIM, there still exists a discrepancy between experimental data and computed results. In this study, we provide a greatly improved precision of estimations using the LISE++ code by evaluating the energy loss straggling of the alpha particles at 5.486 MeV in Tb, Ta, and Au materials. After comparing with the observables, it was found that the ratio of the energy loss straggling computed by the LISE++ code to that measured in experiments has a fairly large range of 1.5 - 3.0. For this reason, the so-called modified LISE++ calculation is constructed by adding the adjusting parameters into the original estimation to minimize the uncertainty of the straggling prediction. The modified calculation has shown dramatic improvements in computed energy loss straggling, which are almost similar to those obtained in the measurements, of 5.486-MeV alphas in the aforementioned materials with the atomic numbers in a range of Z = 65 – 79.
Introduction
In nuclear experiments using radioactive-ion (RI) beams for studies of low-energy reactions, the energy loss and energy loss straggling of the beams in the beam-line materials play a crucial role in the precision of the measured parameters such as the reaction energy, the cross section, and so on. These quantities must be paid attention in the in-flight RI beam production 2 , 1 at accelerator facilities and in the studies of nuclear reactions in inverse kinematics using the thick gas-target approach 5 , 4 , 3 . Notice that thin foils are usually equipped as windows of the target gas cells and gas detectors of the beam optics in such experiments. The energy loss straggling is always considered much smaller than the expected energy resolution of the measurements. Therefore, the energy loss and energy loss straggling are often estimated using computer codes such as LISE++ 7 , 6 and SRIM 9 , 8 ahead of conducting real measurements to optimize energy and necessary thicknesses of the foils used in the experimental setup. Hence, a highly precise calculation of these quantities is always necessary.
Since the models of the energy loss and energy loss straggling calculation strongly depend on various parameters including the incident beam energy and the atomic properties of the materials, there still exists a large discrepancy between the calculations and measurements. To reduce the discrepancy, the parameters related to target materials must be calculated accurately. For example, the average exciting potential and the density correction of absorbers impact on the precision of the straggling estimated by the formula proposed by Bethe-Bloch 10 . This leads to improvements in the models and semi-empirical formulae such as the works conducted by Bohr 12 , 11 , Lindhard and Scharff 13 , Bethe and Livingston 14 , Yang et al. 15 , and Titeica 16 . However, none of the models or formulae is available for every material and beam energy due to the limitations of theories. Since computer codes have been developed by using such models and semi-empirical formulae, their calculations result in a large uncertainty. Therefore, the discrepancies between measured data and theoretical calculation certainly exist and computer codes should be improved to provide a better prediction. In the present study, we evaluated the energy loss straggling calculation of the LISE++ code by considering the calculated results and the measured data obtained by S. Kumar et al. 17 of alpha particles at 5.486 MeV in various foils of Tb (terbium, Z = 65), Ta (tantalum, Z = 73), and Au (gold, Z = 79). We also modified the LISE++ estimations to provide major improvements in the accuracy of such calculations.
Evaluation framework
The energy loss straggling and energy loss of alpha particles with the incident energy of 5.486 MeV in terbium, tantalum, and gold foils were theoretically calculated by using the LISE++ code. The inputs of atomic numbers of the target materials and the thicknesses were varied following the values used in the experiment conducted by S. Kumar et al . 17 to investigate the two quantities of interest. We employed the observed data 17 to assess the uncertainty of the code and then normalized the theoretical estimation of the LISE++ code. To compare the changing rate of the straggling, we also considered the dependencies of the straggling on the fractional energy loss and the target thickness.
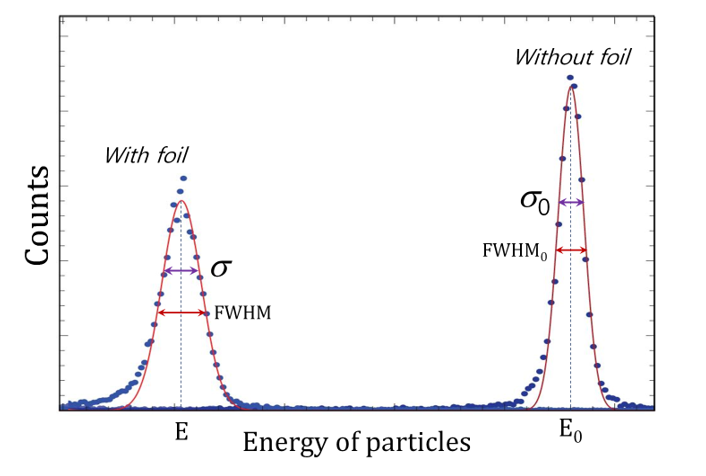
Figure 1 . (Color online) An illustration of the energy spectra before and after thin foils in an energy loss measurement.
In principle, to measure the energy loss and energy loss straggling, the energy spectra of the alphas before and after penetrating through the foils are recorded, as can be seen in Figure 1 . The energy loss and energy loss straggling are deduced based on the differences in the peak centroids and peak widths. The fractional energy loss is defined as the ratio of the energy loss to the incident energy ( E 0 ), which given as
where E is the residual energy of alpha particles after interacting with the materials. The widths are defined as the standard deviation ( ) or the Full Width at Half Maximum ( FWHM ) of the Gaussian distribution of the spectra before and after the foils as
or
where the relationship between FWHM and is given by
In the LISE++ code, a function of the total energy loss distribution along with the target thickness, which is divided into n layers with a thickness of , is used for formulating the energy loss straggling as
where dE / dx is the differential energy loss in each divided layer. Since the LISE++ code generates the straggling in the standard deviation of the Gaussian distribution of the energy loss, we evaluated the experimental straggling based on 1 by using the conversion in in this study.
Results
Table 1 presents the experimental and the computed fractional energy loss, original and normalized energy loss straggling generated by the LISE++ code, and the ratios of straggling taken from the experiment to those deduced by the LISE++ code corresponding to the materials and thicknesses of the foils. The fractional energy loss estimated by the LISE++ code is approximately 5% deviated from the experimental data, which strongly recommends using this code for calculating the energy loss. In contrast, there is a large difference between the experimental energy loss straggling and those estimated by the computer code. In particular, the measured straggling is a factor of about 1.5 – 3.0 larger than the LISE one.
| Foils | Thickness (mg/cm2) | LISE++ | Kumar et al.17 | ΩExp.ΩLISE | ΩMod.LISE(keV) | ΩExp.ΩMod.LISE | ||
| ∆E/E0 (%) | ΩLISE(keV) | ∆E/E0 (%) | ΩExp.(keV) | |||||
| 65Tb | 4.20 | 22.20 | 34.56 | 22 | 59.87 | 1.7 | 77.62 | 0.8 |
| 5.59 | 30.20 | 40.98 | 29 | 87.90 | 2.1 | 98.99 | 0.9 | |
| 8.70 | 49.78 | 55.45 | 48 | 135.46 | 2.4 | 147.17 | 0.9 | |
| 10.93 | 65.84 | 67.61 | 64 | 154.56 | 2.3 | 187.65 | 0.8 | |
| 13.34 | 85.82 | 79.86 | 85 | 219.53 | 2.7 | 228.44 | 1.0 | |
| 73Ta | 4.75 | 22.10 | 36.33 | 22 | 78.56 | 2.2 | 83.51 | 0.9 |
| 5.63 | 26.50 | 40.10 | 26 | 99.36 | 2.5 | 96.06 | 1.0 | |
| 7.50 | 36.21 | 47.80 | 36 | 120.17 | 2.5 | 121.70 | 1.0 | |
| 11.60 | 59.89 | 65.46 | 60 | 176.65 | 2.7 | 180.49 | 1.0 | |
| 13.40 | 71.67 | 74.01 | 72 | 209.77 | 2.8 | 208.96 | 1.0 | |
| 79Au | 4.65 | 20.06 | 35.58 | 21 | 85.77 | 2.4 | 81.01 | 1.1 |
| 5.93 | 25.98 | 40.93 | 27 | 127.39 | 3.1 | 98.83 | 1.3 | |
| 8.30 | 37.47 | 50.44 | 40 | 152.02 | 3.0 | 130.49 | 1.2 | |
| 10.72 | 50.21 | 60.72 | 52 | 176.65 | 2.9 | 164.71 | 1.1 | |
| 14.25 | 71.48 | 78.73 | 74 | 224.63 | 2.9 | 224.67 | 1.0 | |
| 16.01 | 83.41 | 83.19 | 87 | 261.57 | 3.1 | 239.52 | 1.1 | |
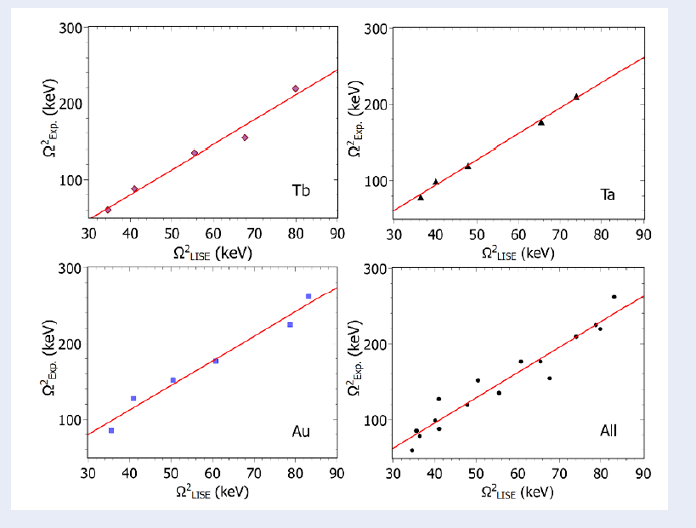
On the other hand, we also investigated the correlations between the straggling and the fractional energy loss or the thickness of the examined foils based on the data presented in Table 1 . We found that the straggling is almost directly proportional to the fractional energy loss with average rates of 3.0 keV/% and 8.0 keV/% for the calculations and experiments, respectively. Similarly, the straggling is almost linearly changed by the thickness with average rates of 6.5 keV/(mg.cm -2 ) and 38.5 keV/(mg.cm -2 ) for the LISE++ and observed data, respectively. These results, which are shown in Figure 2 , indicate that the measured straggling is rapidly increasing with the thickness (right panel) or energy loss (left panel), which is different from the LISE++ prediction.
As aforementioned that the LISE++ straggling is not accurate as the experimental one. Therefore, we tried to fit the data measured by Kumar et al . and used these fitting parameters to correct the calculated straggling as
where a and b are the fitting parameters. The normalized results are shown in Figure 3 with the adjusting parameters listed in Table 2 .
Figure 2 . (Color online) The normalization of the LISE++ calculation based on the experimental data. The red curves are the linear-fitting lines.
| Foils | a | b | R2 |
| Au | 3.22861 ± 0.27868 | -16.77645 ± 16.98651 | 0.97106 |
| Ta | 3.34379 ± 0.11879 | -39.44964 ± 6.50146 | 0.99246 |
| Tb | 3.27996 ± 0.30329 | -51.20384 ± 17.63056 | 0.97499 |
| All | 3.32932 ± 0.24445 | -37.44237 ± 14.22296 | 0.95177 |
Discussion
The uncertainty of the results calculated by the LISE++ code is increasing with the thickness of the foils. This phenomenon can be explained by the direct integration implemented in the LISE++ code, in which energy loss straggling is calculated by the square root of the sum of the intermediate energy loss value as described in . In this calculation method, the oscillation of the bound classical electrons and the atomic density and are assumed to be unchanged throughout the foils, which is not entirely true for the real materials. Since both energy loss and energy loss straggling strongly depend upon the incident energy of projectiles, the atomic and mass numbers of the targets, the larger straggling can be observed in higher atomic numbers of the target materials, as can be seen in Table 1 .
We found that the straggling calculated by the LISE++ code linearly depends on the energy loss. This behavior is also exhibited in the experimental data reported by Kumar et al . 17 . However, the measured magnitudes are much larger than the LISE++ calculations. In contrast to the above cases, the models of Bohr 12 , 11 , Lindhard and Scharff 13 , Bethe and Livingston 14 , Yang et al . 15 , and Titeica 16 generally proposed a nonlinear dependence of the energy loss straggling on the energy loss. This difference is due to the uncertainty of the mean ionization potential on account of the deviations of the energy level of subshells, the number of electrons, and the binding energy of the ionization electrons in the target materials 19 , 18 , 17 . The linear behavior of the LISE++ calculation states that this code remarkably gets over such limitations of the theoretical models. It should be paid attention that the LISE++ code is the combination of the ATIMA code 20 , and Ziegler code 21 , and the database of stopping power taken from the study conducted by F. Hubert et al . 22 .
Figure 3 . (Color online) The energy loss straggling as a function of the fractional energy loss (left panel) and the thickness of targets (right panel). The dashed and dotted lines are to guide the eyes. The modified results of LISE++ (red-square marks) are almost similar to the experimental data (circle symbols).
The present study provides a better prediction of the straggling computed by the LISE++ code using adjusting the parameters determined by the normalization based on the measured data into the LISE++ results, as shown in the last three columns in Table 1 . The modified LISE++ calculation is almost similar to the measured data as can be seen in Figure 3 and the last column in Table 1 . By comparing the data measured by Kumar et al . 17 with the original and modified energy loss straggling values, we found that the discrepancy between the two straggling results is reduced by an average of 3.0 times after adjusting parameters in Table 2 . It should be emphasized that the parameters in this modification are only applicable for alpha particles with the incident energy around 5.486 MeV in the materials with the atomic numbers in a range of Z = 65 – 79. Consequently, to validate the LISE++ code, experiments should be performed for a wider range of incident energy of various projectiles in different targets.
Conclusion
In the present study, we examined the uncertainty of the energy loss straggling by comparing the values calculated by the computer code LISE++ and those reported by Kumar et al . The results have shown that the LISE++ energy loss straggling of alpha particles at 5.486 MeV in various materials of Tb, Ta, and Au has far deviated from the experimental ones. Therefore, to reduce such variation in the straggling, we modified the LISE++ by adding adjusting parameters in respect to the foil materials. In addition, the results indicate that the calculation of the energy spread of alpha particles should be carefully considered when using the code. In summary, our study presents a modification in the straggling calculation of the LISE++ code which generates better straggling values close to the experimental data. This finding has important implications for further uses of the code. Therefore, we strongly suggest that further experimental investigations should be done for other materials to validate the adjusting parameters correcting in the LISE++ calculation.
Abbreviations
RI : rare-isotopes or radioactive ions
FWHM : Full Width at Half Maximum
: standard deviation of the Gaussian distribution
Competing interests
The authors declare that there is no conflict of interest regarding the publication of this article.
Authors’ contributions
The idea of the study, data analysis, and writing manuscript were performed by Dr. Nguyen Ngoc Duy (corresponding author). The results were discussed by Dr. Nguyen Nhu Le. The energy loss was calculated by Nguyen Kim Uyen.
Acknowledgments
We would like to thank Dr. H.T. Phuong-Thao for her valuable discussion and comments. This work was supported by the Vietnam Government under the Program of Development in Physics toward 2020 (Grant No. DT-DLCN.02/19). This work was also funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant Numbers of No. 103.04.2018.303 and No. 103-04.2017.323.
References
- Blumenfeld Y., Nilsson T., Van Duppen P.. Facilities and methods for radioactive ion beam production. Phys Scr T. 2013;152:014023. View Article Google Scholar
- Villari A.C.. Production of RIB: methods and applications. Rev Mex Fis. 2006;52:95-102. Google Scholar
- Artemov K.P., Belyanin O.P., Vetoshkin A.L., Wolskj R., Golovkov M.S., Goldberg V.Z.. Effective method of study of alpha-cluster states. Soviet Journal of Nuclear Physics-USSR. 1990;52(3):408-11. Google Scholar
- Duy N.N., Chae K.Y., Cha S.M., Yamaguchi H., Abe K., Bae S.H.. Beam production of 18Ne with in-flight method for alpha scattering at CRIB. Nucl Instrum Methods Phys Res A. 2018;897:8-13. View Article Google Scholar
- Duy N.N., Kubono S., Yamaguchi H., Kahl D., Wakabayashi Y., Teranishi T.. Low-energy radioactive ion beam production of 22Mg. Nucl Instrum Methods Phys Res A. 2013;897:99-101. View Article Google Scholar
- Kuchera M.P., Tarasov O.B., Bazin D., Sherrill B.M., Tarasova K.V.. Plans for performance and model improvements in the LISE++ software. Nucl Instrum Methods Phys Res B. 2016;376:168-70. View Article Google Scholar
- Kuchera M. P., Tarasov O. B., Bazin D., Sherril B., Tarasova K. V.. LISE++ software updates and future plans. Journal of Physics: Conference Series. 2015;664(7):072029. View Article Google Scholar
- Ziegler J. F., Biersack J. P.. The stopping and range of ions in matter. Treatise on Heavy-Ion Science. 1985;:93-129. View Article Google Scholar
- Ziegler J.F., Ziegler M.D., Biersack J.P.. SRIM\textendashThe stopping and range of ions in matter (2010). Nucl Instrum Methods Phys Res B. 2010;268(11):1818-23. View Article Google Scholar
- Pitarke J.M., Ritchie R.H., Echenique P.M., Zaremba E.. The Z13 Correction to the Bethe-Bloch Energy Loss Formula. Europhys Lett. 1993;24(7):613-9. View Article Google Scholar
- Bohr N.. The penetration of atomic particles through matter. . 1948;Volume 18:. Google Scholar
- Bohr, N. (1953). The penetration of atomic particles through matter (Vol. 8). I Kommission hos Ejnar Munksgaard.. . ;:. Google Scholar
- Lindhard J., Scharff M., Schiott H.E.. K. Dan. Vidensk. Selsk, Mat. Fys. Medd. 1963;33:1. Google Scholar
- Livingston M.S., Bethe H.A.. Nuclear dynamics, experimental. Rev Mod Phys. 1937;9(3):245-390. View Article Google Scholar
- Yang Q., O'Connor D.J., Wang Z.. Empirical formulae for energy loss straggling of ions in matter. Nucl Instrum Methods Phys Res B. 1991;61(2):149-55. View Article Google Scholar
- Titeica S.. Sur les fluctuations de parcours des rayons corpuscularies. Bull. Soc. Roumaine Phys. 1939;38:81-100. Google Scholar
- Kumar S., Sharma V., Diwan P.K.. Energy loss straggling of α-particles in Tb, Ta and Au metallic foils. Vacuum. 2018;158:42-7. View Article Google Scholar
- Kumar S., Diwan P.K., Kumar S.. Energy loss straggling for α-particles in varying thicknesses of Al, Ti and Ni metallic foils. Radiat Phys Chem. 2015;106:21-5. View Article Google Scholar
- Sigmund P.. Low-speed limit of Bohr's stopping-power formula. Phys Rev A. 1996;54(4):3113-7. View Article PubMed Google Scholar
- Geissel H., Scheidenberger C., Malzacher P., Kunzendorf J., Weick H.. ATIMA, GSI. . ;:. Google Scholar
- Ziegler J. F., Biersack J. P.. The stopping and range of ions in matter. Treatise on Heavy-Ion Science. 1985;:93-192. View Article Google Scholar
- Hubert F., Bimbot R., Gauvin H.. Range and stopping-power tables for 2.5\textendash500 MeV/nucleon heavy ions in solids. At Data Nucl Data Tables. 1990;46(1):1-213. View Article Google Scholar
