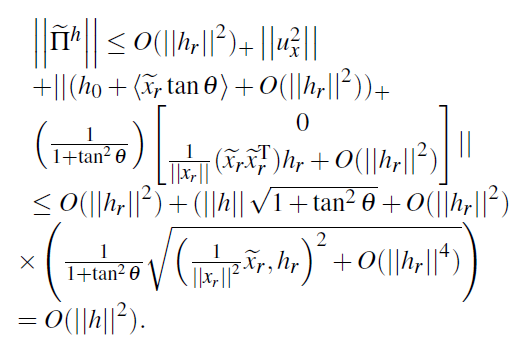
On the calm b-differentiability of projector onto circular cone and its applications

Abstract

In this paper, we study a concept on the calm B-differentiability, a new kind of generalized differentiabilities for a given vector function introduced by Ye and Zhou in 2017, of the projector onto the circular cone. Then, we discuss its applications in mathematical programming problems with circular cone complementarity constraints. Here, this problem can be considered to be a generalization of mathematical programming problems with second-order cone complementarity constraints, and thus it includes a large class of mathematical models in optimization theory. Consequently, the obtained results for this problem are generalized, and then corresponding results for some special mathematical problems can be implied from them directly. For more detailed information, we will first prove the calmly B-differentiable property of the projector onto the circular cone. This result is not easy to be shown by simply resorting to those of the projection operator onto the second-order cone. By virtue of exploiting variational techniques, we next establish the exact formula for the regular (Fréchet) normal cone (this concept was proposed by Kruger and Mordukhovich in 1980) to the circular cone complementarity set. Note that this set can be considered to be a generalization of the second-order cone complementarity set. In finally, the exact formula for the regular (Fréchet) normal cone to the circular cone complementarity set would be useful for us to study first-order necessary optimality conditions for mathematical programming problems with circular cone complementarity constraints. Our obtained results in the paper are new, and they are generalized to some existing ones in the literature.