Dynamics of a contracting fluid compound filament with a variable density ratio
- Faculty of Vehicle and Energy Engineering, Phenikaa University, Hanoi, Vietnam
- Graduate University of Science and Technology, Vietnam Academy of Science and Technology, 18 Hoang Quoc Viet, Cau Giay, Hanoi, Vietnam
Abstract
Introduction: Compound fluid filaments appear in many applications, e.g., drug delivery and processing or microfluidic systems. This paper focuses on the numerical simulation of an incompressible, immiscible, and Newtonian fluid for the contraction process of a fluid compound filament by solving the Navier-Stokes equations. The front-tracking method is used to solve this problem, which uses connected segments (Lagrangian grid) that move on a fixed grid (Eulerian grid) to represent the interface between the liquids.
Methods: The interface points are advected by the velocity interpolated from those of the fixed grid using the area weighting function. The coordinates of the interface points are used to construct the indicators specifying the different fluids and compute the interfacial tension force.
Results: The simulation results show that under the effects of the interfacial tension, the capsuleshaped filament can transform into a spherical compound droplet (i.e., non-breakup) or can break up into smaller spherical compound and simple droplets (i.e., breakup). When the density ratio of the outer to middle fluids increases, the filament changes from non-breakup to breakup upon contraction.
Conclusion: Increasing the density ratio enhances the breakup of the compound filament during contraction. The breakup is also promoted by increasing the initial length of the filament.
Introduction
Nowadays, compound droplets have been used in various applications, such as drug distribution,1 microfluidic system,2 food processing technology,3 etc. During the breakup of the droplets, the fluid filaments can be formed with primary droplets. The contraction of these filaments creates more droplets. The breakup processes of the single fluid filament have been investigated for a long time. Thus, its knowledge has become mature.4
Concerning compound droplets, many studies have been done, such as numerical simulation of dynamical behaviors of compound droplets,5, 6 the collision of compound droplets,7, 8 and the deformation and breakup of compound droplets in shear flow.9 The initial conditions of the problem are significantly important, depending on the surface tension of the interface separating different fluids, the properties of the fluids such as viscosity and density.
Unlike compound droplets, compound filaments have not been considered so far. Accordingly, numerical studies of a contracting compound filament still lack in the literature. Thus, to provide such lacking knowledge, the present study aims to enhance understanding of dynamical behaviors of the compound filament when it contracts in an initially passive environment undergoing the influences of the fluid properties via numerical simulations. Two considered parameters for the deformation and breakup of fluid compound filament include the density ratio between the outer fluid and the middle fluid and the initial aspect ratio of the filament. This is a new problem that has not been explored in the literature. The method used in this work is a front-tracking method for multi-fluid and multi-phase flows.10
This paper is structured as follows: the introduction section gives an overview of research papers related to fluid compound filaments, the numerical model and method section gives the mathematical formulation, the numerical method, and the dimensionless parameters governing the problem. The result section presents some typical results. The discussion section provides discussion about the numerical results. The conclusion and future development are presented in the conclusion section.
Numerical model and method
The entire physical domain of an axisymmetric compound fluid filament is shown in Figure 1a. To save computation time, we consider the upper half of the fluid compound filament and use the axisymmetric configuration with a domain and proper boundary conditions, as illustrated in Figure 1b. The cylindrical coordinate system, in which r and z denote the radial and axial directions, is used for analysis. The following initial conditions are assumed: is the lengths of one-half of the outer and inner fluid filaments, respectively; and are the radius of the outer and inner fluid filaments, respectively. The viscosity and density of the outer, middle, and inner fluids are , and , respectively. Here, gravity is ignored as it plays a very small role. These fluids are assumed to be incompressible, immiscible, and Newtonian. Hence, the interfacial tension coefficient at the interface between the inner and middle fluids is , and that at the interface between the outer and middle fluids is .
It is assumed in this paper that the material properties are constant in each fluid. With numerical computation, three fluids are considered one fluid with viscosity and density changing when traveling through the interface. The Navier – Stokes equations are valid for fluid domains, and a set of equations can be defined for the entire domain, provided that the viscosity and density jumps are computed accurately and the interfacial tension is included. Therefore, the Navier – Stokes equations are represented as below:10, 11

A compound filament contracting in an initially passive environment. (a) The entire physical domain and (b) the computational domain with an axisymmetric configuration.
Where u is the velocity vector, is the pressure, is twice mean curvature, is time, and superscript is the transpose. The interfacial tension force is the force caused by the interfacial tension between two fluids is the interfacial tension coefficient, n denotes the unit normal vector to the interface, denotes the interface of the compound filament, denotes the arc length. is the Dirac delta function that has a value of zero at all points except for the interface point x where the function is equal to one. The fluids are not mixed, and the material properties are constant within each fluid. Hence, the equations of state for density and viscosity are:
Where . Because this problem is investigated with the assumption of incompressible fluids, the continuity equation is represented by:
To solve the problem, we use the front-tracking with finite difference approximations. A finite number of Lagrangian grid points is used to represent the interface among different fluids. These Lagrangian points are laid on a fixed staggered grid, i.e., Eulerian background grid. Integrating the equation below to determine the positions of the discrete interface points (x) moving with the velocity of . is determined by interpolation from the velocities of the four nearest background grid points.
Instead of solving the density directly, we first move the interface between the different fluids and reconstruct indicator functions from its position. Using these indicator functions is to specify the material properties at every location in the domain.12 In particular, we here build two indicator functions and , from the inner and outer interfaces, respectively. equals zero in the inner fluid and one in the other fluids. Similarly, equals one in the outer fluid and zero in the other fluids.9, 11, 13 Accordingly, for example, the density at every location is given as
The positions of these points are also used to calculate the interfacial tension force. To do so, we first compute the force on each front element connecting two adjacent points using the tangents at these points, and we then sum these forces on the entire interface elements. The interfacial tension force is transferred to the background grid using the area weighting function.10 The continuity and momentum equations are approximated by the second-order centered finite difference method for spatial derivatives. Time integration is solved with an explicit, second-order predictor-corrector scheme.
In this study, the middle fluid is chosen as the based fluid because such choice is to better understand and refer to simple filaments4 when, for example, ignoring the presence of the inner fluid (i.e., inner filament). The scaling length is the radius of the outer filament , and the reference time is . Accordingly, the reference velocity is . As a result, the problem dynamics is influenced by dimensionless parameters: denoting the Ohnesorge number, and denoting the initial aspect ratios of the inner and outer filaments, denotes radius ratio between inner and outer filaments; and denoting the density ratios, and denoting the viscosity ratios, and denoting interfacial tension ratio between inner and outer filaments.
The dimensionless time is
Result
In this study, a typical grid resolution of 192576 grid for a domain = 4 12 is used in the simulation model to perform = 10. Such a grid solution is selected through a grid refinement study (not shown here), and it is found that the 192576 grid gives results without variance in the compound fluid filament shape as compared to those obtained using finer grids. A higher (e.g., = 30) requires a larger domain (e.g., = 432) with a higher number of grid points in the axial direction (e.g., 1921538).
To validate the method, we here compare our computational result with that computed by Notz and Basaran4 for the evolution of the shape upon contraction of a simple filament with = 1.0, = 15.0. Other parameters for our computations include = 0.0, = = 0.01, = = = 0.0 and = 0.0 (i.e., simple filament). The comparison is shown in Figure 2. This figure indicates that our prediction is very well agreed with that computed by Notz and Basaran. This comparison confirms our method accuracy.
Because there are many parameters related to the deformation dynamics and the breakup of the filament, in this study, we pay more attention to the density ratio between the outer and the middle fluids () and aspect ratio . Therefore, other dimensionless parameters are fixed in calculations: = 0.1, = = = = 1, = 0.6.
Figure 3 compares the velocity and pressure fields of the fluid filament corresponding to two ratios = 0.8 (left) and = 1.6 (right). At t = 10.08, the inner fluid filament tends to break up into droplets in the case of = 1.6 because the pressure difference between the inner and outer fluids is greater than that in the case of = 0.8, and the velocity field at the neck of = 1.6 has an inward direction while the velocity field of rom = 0.8 has an outward direction. Also, in the case of = 0.8, the inner and outer fluid filaments will inflate at the neck and become a spherical compound droplet. In addition, due to = , in the case of = 1.6, decreases more as compared to the case of = 0.8 (assuming ro remains unchanged). When decreases, the instability of the separating interface increases, and so does the breakup possibility of the filaments.14

Comparison of a contracting simple filament between the present result and that reported by Notz and Basaran4. At each time, Notz and Basaran’s prediction is shown in the upper half and our prediction is shown in the lower half. The parameters are shown in the text.
Figure 4 shows the change in the shape of the fluid compound filament by time, from = 0 to = 25.9. The shape of the compound fluid filament changes gradually, from the capsule shape at the beginning to the bone shape at = 8.12. At = 9.38, the inner filament has a similar shape to an hourglass. The inner filament is expected to break up; however, at = 10.36, it inflates at the middle, and in the end, at = 25.9, the inner and outer fluid filament becomes spherical fluid droplets which are called a spherical compound fluid droplet.

The form of the compound filament at time
Figure 5 shows that when the density ratio between the outer and middle fluids is increased to = 1.6, the breakup of the inner fluid filament happens. The shape of the filament changes from capsule shape to bone shape at = 8.1. At = 10.44, the inner fluid filament nearly breaks up, and at = 10.62, the inner fluid filament performs breakup. As a result, from a capsule-shaped fluid filament, under the action of interfacial tension, contracts lead to the breakup of the inner fluid filament and create a compound droplet containing two cores (at = 27.72).
Thus, based on analysis of the pressure field, velocity field, and deformation of the fluid filament over time, it is shown that the contraction and breakup of the fluid compound filament are influenced by the density ratio of the outer and middle fluids. For example, in the case of = 10, when changes from 0.1 to 6.4, the inner fluid filament breaks up when ≥ 1.6.
Discussion
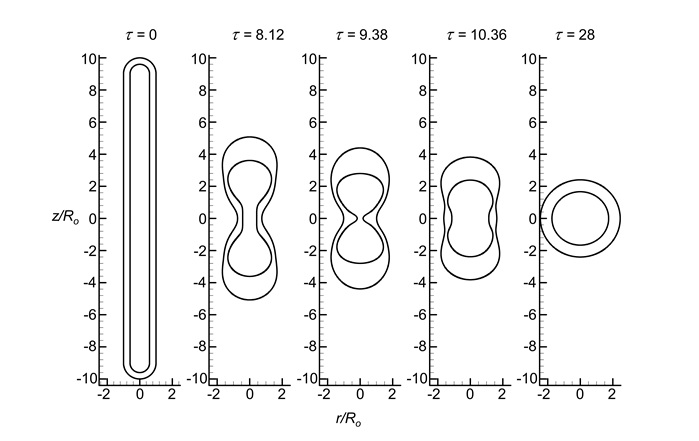
Deformation of the compound fluid filament over time in the case of

Deformation of the compound fluid filament over time in the case of
The effect of the density ratio () on the deformation parameter of a compound fluid filament
Figure 6 (a) and (b) show the effect of the density ratio between outer and middle fluids () on the deformation parameters of the inner and outer filaments.
Where and are the deformation parameter of the inner and outer fluid filaments, respectively. and are the radial coordinate of the furthest point on the outer and inner interfaces. and are the axial coordinate of the furthest point on the outer and inner interfaces, respectively.
The results show that when decreasing the density ratio , the retraction rate of the inner and outer filaments increases. In the non-breakup ( = 0.2 and 0.8), the deformation parameter is varied from positive to a negative value, and its value is equal to zero when the filament recoils to a spherical shape at the end of the contraction process. In the case that the inner filament breaks up into two droplets at the center position of the filament, the deformation parameter of the inner one vanishes after the breakup (the pink delta line in Figure 6 (a) and (b)).

(a) The deformation parameter of the outer fluid filament over time
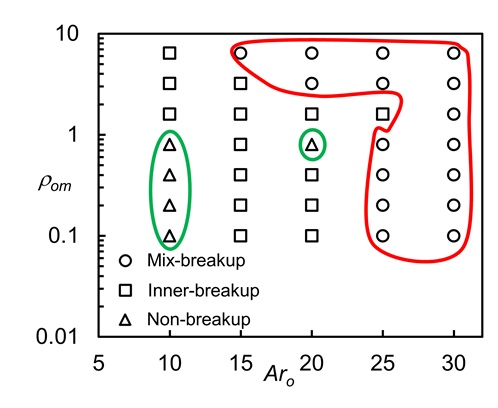
The phase regime of the deformation and breakup of the compound filament. The other parameters are provided in the text.

The deformation of the compound fluid filament over time in the case of
The effect of the density ratio () on the breakup of a compound fluid filament
To evaluate the entire figure of the contraction process of the compound filament. We varied the aspect ratio of the outer filament () from 10 to 30 and the density ratio from 0.1 to 6.4. The phase regime of the deformation and breakup of the compound filament is presented in Figure 7.
We found that after contraction, the compound filament has three pattern modes as follows: the non-breakup mode as shown in Figure 4, the inner breakup mode as shown in Figure 5, and the mix-breakup mode as shown in Figure 8. As indicated in Figure 7, on the left side of the regime diagram, the non-breakup mode represented by triangle symbols is zoned by a green line. On the right side, the mixed breakup mode appears with circle symbols zoned by a red line. The remaining cases, represented by square symbols, correspond to the breakup of the inner filament while the outer filament is non-breakup. It is clear that increasing the density ratio and increasing the initial length of the filament promote the breakup of the compound filament upon contraction.
Conclusions
Research results show that the fluid density has an essential influence on the deformation or the breakup of the fluid compound filament. Accordingly, the lower the density ratio of the outer and middle fluids ( < 0.8) and the lower aspect ratio ( = 10) lead to the fluid compound filaments contracting to a spherical compound droplet (i.e., non-breakup mode). The contraction of the inner and outer filaments mostly breaks up when the aspect ratio of the outer filament is high ( = 25-30). The remaining cases correspond to the breakup of the inner fluid filament (Figure 7). All compound filaments, whether or not breakup, tend to return to the spherical shapes at the end of the contraction process due to the effect of interfacial tension.
This study is very important for desirable compound droplet control in biomedical technology or some other applications. Therefore, the present study helps to select the treatment process through the initial conditions to form compound droplets containing two or more cores or prevent breakup of the filament.
The present study is limited to the compound filament that contains one inner filament. However, in many applications, e.g., microfluidic systems,15, 16 the filament can enclose two or more inner interfaces. In some other situations, the filament dynamics can be affected by contaminants17 or the temperature field.18 Such complicated issues should be addressed in the future studies of the contracting compound filament.
Conflict of interest
The authors declare that they have no competing interests.
Authors contribution
Vinh T. Nguyen: Investigation, Visualization, Formal analysis, Writing- Original draft
Truong V. Vu: Conceptualization, Methodology, Writing- Reviewing and Editing, Supervision
Phan H. Nguyen: Conceptualization, Supervision
Nang X. Ho, Binh D. Pham, Hoe D. Nguyen and Hung V. Vu: Investigation, Formal analysis
Acknowledgments
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 107.03-2019.307.

