AiMA - An AI-Based Mobile System to Assist College Students with Math-Related Issues

Abstract

Introduction: As technology continues to progress, the importance and influence of mathematics in people's lives are growing. The emergence of mobile systems has brought about several benefits, such as portability, convenience, and accessibility, especially in the field of education. It is crucial to develop a mobile system that can cater not only to high school students but also to those enrolled in colleges and universities, offering solutions for basic calculations and highly specialized algorithms. To address this need, this research presents AiMA, an AI-based mobile system that assists college students with math-related issues.

Methods: In this paper, we discuss the limitations of current math-solving mobile applications and propose a solution that caters to specialized algorithms for university students. AiMA employs React Native on the front-end side to render the user interface and Flask-server on the back-end side to handle numerical data. Additionally, an AI model is implemented to handle input images stored in a cloud-based media management platform for detection.

Results: The system's functionality evaluation indicates that AiMA provides advantages over existing solutions by enabling users to solve complex calculus problems and receive tailored solutions for specific areas of mathematics.

Conclusion: This makes AiMA a highly valuable tool for college and university students who require specialized assistance with their math-related studies.

Introduction

A mobile application (“app") is often used to describe programs for mobile devices, such as smartphones and tablets. The most significant difference between traditional desktop and mobile applications is that the application running on a mobile device can be achieved from the app store. Most devices automatically install apps when downloaded, which creates a seamless installation process for the user. In addition, most mobile applications are low-cost because they need to be more advanced and require fewer resources to develop. However, apps may offer less capability than desktop programs due to the limitations of the mobile operating system (such as iOS or Android). Nevertheless, the app field has become the trend in the developing community due to its portable, small-size, easy-to-use, and quick-response features. With the knowledge of mobile techniques, generating an application to tackle the practical issues that exist is significant. An outstanding area that can be focused on is education, especially mathematics.

With the development of technology, the significance and impact of mathematics on people's lives are growing daily. Students' views on the role of mathematics in their future studies and careers will be influenced by changes in the mathematics learning environment and their conceptions of the subject. This will ultimately affect how they perceive the relevance of mathematics in their future studies and careers 1 . According to the research of Sven Ove Hansson 2 , mathematics is crucial in developing modern technology and innovation. Many technological advancements, such as artificial intelligence, machine learning, and cryptography, rely on mathematical concepts such as calculus, statistics, and linear algebra. Developing a system that can solve basic calculations while providing solutions for highly specialized algorithms catering to high school students and those enrolled in colleges and universities and beyond is crucial. Most recent mathematics mobile applications, which are just publicly available, have focused only on familiar and fundamental areas in mathematics, such as calculus or trigonometry. Our research aims to fill in the current gap in the field.

In this research, we introduce AiMA, an AI-based mobile system that assists college students with math-related issues. Our mobile system will be applied to the client-server architecture to generate the mobile application. In detail, React Native is used on the front-end side for rendering the user interface (UI) and optimizing the user experience (UX). Meanwhile, on the back-end side, the Flask server is applied, known as one of the most effective servers for handling the numerical data to modify and calculate the input. Regarding feature diversification to enhance user experience, an AI model is implemented to handle the input image stored in a cloud-based media management platform (Cloudinary) for detection.

This project stands out from others due to its distinctive and innovative characteristics. Unlike the existing mathematics software applications, all fields in AiMA are more clearly and intuitively divided to create convenience for end-users. Furthermore, realizing the user’s need for specialized mathematics fields and highly applicable algorithms is something that other programs have either been unable to perform or have been able to do but have not been well optimized. In addition, AiMA mainly focuses on performance. Therefore, the response time and execution time are optimized to minimize user interaction time with the application. Moreover, all of the applied technologies in this application are free to low cost. Hence, AiMA is comparable to current mathematics applications with the free-for-charge characteristic.

The following are the main characteristics of AiMA:

• Convenience: Design an application with a portable feature.

• Content quality: Generate an application covering a wide range of topics, from basic arithmetic to advanced algorithms.

• Performance: The performance can be manipulated by applying some methods, such as reducing image or video size, caching, and minimizing network requests.

• Cost: The app should be affordable or free to use. If so, more customers can be reached.

The functionality evaluation indicates the ability of the system to correctly calculate not only the simple but also the compound expression within a desirable response time.

Background and Related Research

Background

Technologies in mathematics app

The client-server architecture in a mathematics app facilitates effective and scalable data management and communication between the app’s users (clients) and the app’s server. The functionality and resources of the software are split between two entities, the client and server. The server is a distant or local computer that stores and processes data, whereas end-user devices such as smartphones or computers can perform the client. In detail, the client-server architecture creates communication between two entities for exchanging data via the HTTP protocol without interruption. In this research, the server will handle the input data, which can be the string or image format equation received from the user’s device. The server must carry out the specified operations to return the accurate final results after responding to the client for the user’s receipt. It is mindful that the server side will tackle the calculations, and the time for each user request will decrease. Therefore, it is considered wise to implement this architecture in mathematics software.

Since AiMA is an AI-based system, this software must incorporate an OCR AI model. Optical Character Recognition (OCR) is a technology that extracts characters from printed or imaged text and converts them into machine-readable code. The process of identifying characters from photos or text includes the OCR model, which is a component of the OCR system. Machine learning techniques create traditional OCR models, intense learning models such as convolutional neural networks (CNNs) or recurrent neural networks (RNNs). To classify and identify various characters, these models are trained on enormous amounts of character-containing images by labels. One of the key advantages of integrating an optical character recognition model into math software is the ability to recognize mathematical symbols, equations, and expressions. First, integrating the OCR model into a math application helps users enter data more naturally and flexibly. Users can write or type natural calculations, and the OCR model will recognize and transform text, rather than only depending on manual input or predefined characters into a computer. The OCR model will convert the captured content into a digital format, saving time and effort compared to retyping the calculation. With the application of this model, the user experience can be highly enhanced.

Mathematics fields in AiMA

Theoretical models in computing (TMC) refers to mathematical or abstract models that rely on the knowledge of numerical methods. Numerical methods are applied to solve mathematical problems in various fields that conventional mathematical equations or classical methods cannot tackle. This model applies numerical and computational techniques instead. The following problems are addressed using techniques:

Many fields in numerical methods that AiMA mainly focuses on for development can be mentioned. First, the optimization method is one of the most important methods used for iteratively searching the optimal values of a function. The primary purpose of this is to determine the independent variable so that the function can reach the minimum or maximum value. As mentioned above, AIMA focuses on developing applied algorithms and is dedicated to IT students, so optimization methods can be used to optimize the parameters in the machine learning model. The parameter's optimal value improves the model's performance and accuracy. There are many algorithms for this method, for instance, the Newton method, golden-section search method, and interpolation method. The following field is ODE, which stands for ordinary differential equation. In the numerical method, the ODE method is a set of algorithms used for solving the original derivative equation by determining the approximate value of the function in a definite interval of independent variables. There are different ODE methods in numerical methods, including simple methods such as Euler and advanced methods such as Runge‒Kutta. Furthermore, differential and integral methods (Raphson method, Simpson ⅛ rule, Simpson ⅜ rule, etc .) and curve fitting methods (linear regression, multilinear regression, etc .) are all supported for the calculation. The benefits of using numerical methods instead of conventional methods are that using analytical techniques can be challenging or impossible to solve some issues precisely. Their solutions can be approximated using numerical approaches. For instance, one can estimate complicated integrals using quadrature techniques such as Simpson's rule, trapezoid rule, and Romberg's method.

“Probability" is a branch of mathematics that examines the possibility that an event will occur. It entails calculating the likelihood of an event occurring or not occurring based on available information. Several applications in the field of IT make extensive use of probability theory, which can be followed by varying the appliances of artificial intelligence (AI), such as natural language processing, image processing, and robotics. While “Statics" has been applied in the data science area to analyze and interpret data, its primary function is to draw conclusions from collected data and predict what is next. In addition, it is an efficient tool for helping bots determine extensive data with random noise. Some outstanding concepts of Probability, Statistics, and Random processes that we can apply to solve technology-related problems:

• Hypothesis Testing: a statistical method used to test a hypothesis or claim about a population parameter using sample data.

• Bayes' Theorem: This theorem is used to calculate the conditional probability of an event based on prior knowledge of related events.

• Counting and conditional probability are essential concepts in probability theory and statistics. The likelihood of an event happening is examined in conditional probability based on the possibility of an earlier event happening. The first event determines the second event.

In addition, calculus and geometry are the fundamental topics of math. First, calculus is an advanced math subject often taught in the early years of university programs. It includes two essential contents: differential calculus and integral calculus. The differential operations are concerned with the derivative and the instantaneous change in the value of a function. Integral calculus helps students know how to integrate a function, calculate the area of the limit of the curve, etc. However, going to college, the requirements, scope of content, and knowledge of calculus will be more advanced. The student will have to learn a lot of knowledge and complex concepts and how to solve many more difficult problems. This is also why calculus has become an obsession of many students, including students who have approached this subject since high school. Moreover, geometry is a branch of mathematics that addresses questions of shape, size, relative positions of shapes, and properties of space. Geometry includes formulas for length, area, and volume, such as the Pythagorean theorem, circumference, and area of circles, triangles, cylinders, spheres, and pyramids.

In addition, various final products about mathematics mobile applications have been widely published to the end-user. The first app that needs to be mentioned is Photomath from Microblink, which provides a mathematics solver system. This application is only supported on mobile platforms. This is one of the most popular applications in this branch therefore, in 2017, the Tech Edvocate named Photomath among its top 20 teaching and learning apps 3 , and in 2021, the legally constituted business Photomath LLC reported that it had raised $23 million in Series B funding, with Menlo Ventures serving as the lead investor 4 . Photomath is a powerful tool that can solve problems in the only field of calculus. It can quickly find solutions to issues involving integrals, derivatives, etc. However, Photomath has difficulties in solving long and complex expressions. However, a user-friendly interface makes Photomath available to more people. Photomath has a team of R&D (Research and Development) to research mathematics methodologies worldwide to supply the correct solution and ensure that all the shown steps are expert-verified. With sensitive AI techniques, Photomath uses the camera on a user's mobile device to scan and recognize mathematics symbols to solve them. In the early years, Photomath could not identify the handwriting problem, but from 2016 until now, the app began recognizing handwriting in addition to printed text. The fact that Photomath can demonstrate how to solve each problem totally for free is a significant benefit, but the explanations are limited. Due to the student feedback collected, Photomath can be used in the classroom for teaching purposes 5 . In addition, students stated that Photomath provides a visually appealing computational assistance tool with straightforward interaction 6 . Likewise, Israeli businessmen Michal Avny, Adam Arnon, and Lev Alyshayev launched a mathematics mobile application called Symbolab in 2011. This multiplatform application can support users on both mobile and web platforms. However, for the best experience and to use all features of Symbolab, users are encouraged to use the application on mobile devices when the AI scanner is only available on this platform. Users can use the camera on their mobile device to detect the expected mathematics problems. A constraint is that it cannot eliminate redundant characters. Like Photomath, Symbolab can solve problems in calculus. However, this application has a variety of math topics, including geometry, trigonometry, and linear algebra. In addition, Symbolab's step-by-step display system is rated as adequate. Therefore, it has been suggested to be employed as a teaching tool in various studies, including the research paper of Nguyen Viet Duong et al . 7 . Mathway is a different, equally well-liked application. Mathway builds on earlier apps and has a far more comprehensive range of disciplines. In addition to math, Mathway can support physics and chemical formulas. The capacity to answer trigonometrical issues is the most notable 8 , and Mathway has been successful in this area since it offers many formulas in addition to intuitive use. Like SymboLab, Mathway is a multiplatform application with a powerful AI model that can detect handwriting with very high accuracy.

However, the free package is minimal. Users have to unlock the premium package to see the detailed steps, which is opposite to the goal of this paper. After analyzing the abovementioned applications, building upon their advantages while overcoming limitations is vital. Current mathematical applications strongly emphasize creating and using more algorithms in various mathematical fields and beyond. In light of this, developing an application that can solve complex issues makes sense.

AI-Based Analysis

Presently, a math application can be evaluated based on a variety of aspects. It is inadequate to produce an application with an intuitive user interface, good performance, or an affordable price. AiMA aims to enhance the user experience through innovative, clever techniques. Therefore, an AI model, pix2tex, was reused and integrated into this software. Therefore, an AI model was reused and integrated into this software. The analyses below are based on contributions from Lukas Bletcher, who publishes the OCR project for mathematical symbols on GitHub. Although it was developed for a specific purpose, this model's processing steps and procedures can be applied to many other models in the same field.

Data collection

It must be trained using the gathered datasets to create a highly accurate, predictable AI model. The dataset used by our AI model mostly comes from CROHME (Competition on Recognition of Online Handwritten Mathematical Expressions), a widely used dataset in mathematical symbol recognition, including data on online handwriting of mathematical expressions. Doing this ensures that the dataset reflects various mathematical expressions that can be utilized in real-world situations. Numerals, letters, and other mathematical symbols are all present.

Preprocessing image

After receiving the raw dataset, preprocessing of the image data is essential, which is the process of preparing the data before being inputted into the AI model for training or testing. Image preprocessing aims to improve the image data, boost recognition of the character's model performance and reliability, and simplify the model's identification of critical features.

The image preprocessing methods include:

• ShiftScaleRotate and GridDistortion are used to transform the image, create scaling, or rotate the image.

• RGBShift is used to change the color of the image. GaussNoise causes the pixel values in the image to be adjusted for random Gaussian noise, which helps the model learn general features of mathematical expressions without being too dependent on specific details.

• ImageCompression: This transformation reduces the image's compression quality to 95%.

• ToGray: a method to convert RGB images to grayscale images to simplify data by reducing color information in the image but keeping information about the brightness and contrast of pixels.

• Normalize: Normalize image data. The mean of the images is normalized to (0.7931, 0.7931, 0.7931), and the standard deviation is normalized to (0.1738, 0.1738, 0.1738).

• ToTensorV2: Convert the image into a tensor, a form suitable for PyTorch models such as pix2tex.

Model architecture

An AI model, pix2tex, is built based on the Vision Transformation (ViT) architecture. In contrast to other popular architectures, such as CNNs (convolutional neural networks), ViT applies the image sequential image transformation mechanism and a network called Transformer, which is a neural architecture using multihead attention and feed-forward as the networks for handling the critical features of the input image based on comparison with preprocessing data 9 .

ViT architecture divides the image into many ‘patches’ of the same size and converts them into vector embedding 10 . These embeddings serve as inputs to the transformer network, passing through the mentioned neural networks to generate high-level image representations. For the implementation, generating a get encoder function is responsible for initializing and creating a custom version of ViT architecture. This function initializes the backbone by using the deep neural network ResNetV2. Backbone plays a role in extracting features from input images and preparing data for processing the ViT model. Then, the vector embedding received from the backbone will be transformed into patches with small sizes. This model is 16x16 from a 224 px input preprocessed image to fit with the standard size of the transformer network. Finally, a classification layer is used to perform the prediction for the image’s label. Figure 1 indicates the process of the ViT architecture.

Figure 1 . Vision Transformer (ViT) 10 .

An image is divided into fixed-size patches, which are then linearly embedded and processed by a transformer encoder. The model can simultaneously assess many interactions inside the patches because of the multi-head attention mechanism, which captures local and global contexts. Subsequently, the classification head utilizes these features to make accurate predictions, making ViT a robust architecture for image recognition tasks.

Testing and validation

After applying the pix2tex AI library to the project and going through much testing using the AI-scanning feature to solve math problems on AiMA, it can be concluded that the input image is a standard-size screenshot, and the AI model can obtain a positive result of prediction when it returns a latex string with an accuracy up to 95%. However, the accuracy is significantly reduced when applying images that are too large or too small. This demonstrates the effectiveness of the AI model when using the ViT architecture. In contrast, pix2tex faces the problem of handwritten images. When it is a meager prediction accuracy rate with this type of image, this will seriously affect the user experience. An investigation was conducted to determine the cause. The critical outcome is that the model severely needs handwriting picture data, which impacts the dependability of pix2tex. To improve this, we modify and add the necessary data to the model's dataset, and then the model will be retrained again. The fine-tuning knowledge can be applied to add, remove, and edit layers for the model to fit the new dataset 11 .

System Design and Implementation

System Design

In the system design of AiMA, each request from the client should follow a specific process. The three primaries of a fundamental procedure are typically the input, process, and output parts. Each part plays its role. For detail:

Input

The end user has a total of two options

• Use the keyboard to input the problem: the user can manually type the necessary data via the supplied input field in the software.

• Use the camera for AI-scanner: Users can use their device’s camera to capture the image of the expected equation.

The input is sent to the backend server for the following processes.

Process

Depending on the input format, the process will differ:

String input:

• The input string must undergo a validation process to ensure its compatibility and suitability for calculation and pop-up errors if invalid.

• If the input is valid, the back-end server is responsible for checking the type of string for routing it to the correct controller.

• Input will be formatted to match the syntax of the server-side programming language.

• In this step, the server is available to execute the calculator functions to return the final results.

Image input:

• The picked or captured image will be stored in a cloud-based platform to obtain its URL.

• The AI model can read the URL. Pop-up error if an undefined URL.

• The AI model converts the URL into a latex string if the URL is valid.

• The received latex string must be formatted to match the syntax of the server-side programming language.

• It can tackle the string to return the final results.

Output

• The raw received string will be reformatted by the mathematics conversion.

• Navigate the user to a new screen to display the formatted results and specific steps.

Implementation

AiMA was developed primarily on mobile platforms. Therefore, this research is entirely focused on software. The application of the software development process is crucial, and the waterfall development process model is used to develop the system, as shown in Figure 2 . The waterfall development process model is a linear and sequential approach to software development. It consists of several phases, including requirements gathering and analysis, design, implementation, testing, deployment, and maintenance. Each phase must be completed before moving on to the next phase.

Figure 2 . Waterfall development process model .

The figure above depicts the six critical processes of this model. It showcases a step-by-step progression through discrete phases, starting from requirements gathering and progressing through design, implementation, testing, and maintenance after deploying the software product.

A. Requirements & Analysis

In the Requirements & Analysis stages, the project requirements were collected, analyzed, and documented. For details, gathering user requirements is always paramount to start building any software. Hence, conducting a survey can collect the potential customers’ needs. In this research, a small-scale survey was undertaken to learn what the Information Technology and Logistics majors at the International University - Vietnam National University Ho Chi Minh City, Vietnam, wanted from the use of mathematics. Figure 3 indicates students’ interest in areas of need. In this survey, the students from these majors are asked one question. The survey results showed that the students from both groups of majors already knew and often used mathematics learning support applications. According to the general assessment, Mathway was highly appreciated for its variety of topic areas and easy-to-use interface. However, the students responded that the main limitation of many current apps is the lack of support for specialized mathematics fields. Therefore, they want an application to meet this problem. The following is a result from this survey, which shows the most concerned specialized fields:

Figure 3 . The bar chart indicates students’ interest in areas of need .

According to survey findings, university students, as well as those in high school and below, also require assistance in math, particularly in specialized areas. Probability and numerical methods are the two that hold the most appeal among them. Therefore, we will pay attention to and concentrate on developing this sector in order to offer the most excellent solutions.

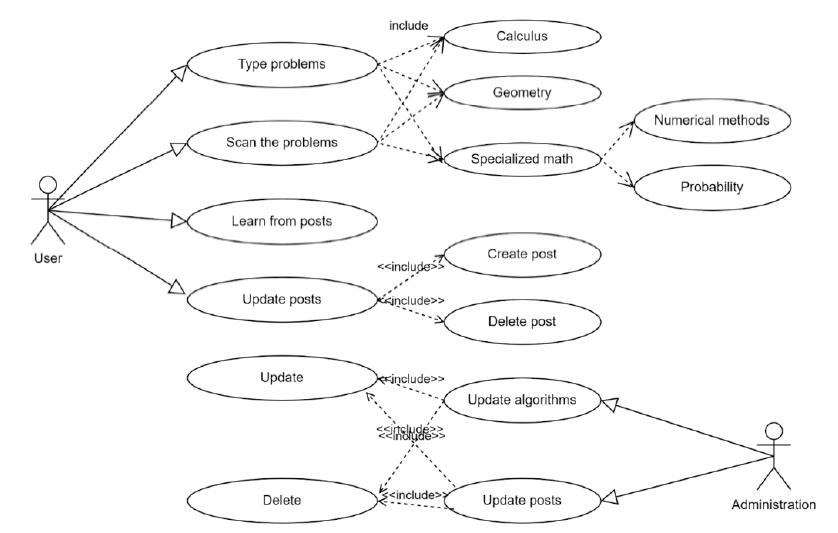
From the above bar chart, combined with the evidence mentioned in the previous sections about the importance and application of digital technology for education, realizing an application that can support specialized problems is a significant concern. Therefore, the features and functions of the software can be identified. Use case diagrams, shown in Figure 4 , are often used in the analysis stage to determine the actor's ability to perform the function through specific use cases, thereby showing the relationship between them. This diagram reflects the original idea about the interaction among users, administration, and the software system. Note that some features are in development and will be published in the future.

Figure 4 . Use case diagram .

The relationship between the user, administrator, and system is depicted in the above-mentioned figure. Users may interact with the system by using computing features as well as CRUD-related activities (create, read, update, and delete) when using the forum feature. Similarly, administrators can take other actions like altering support algorithms or editing user posts. Administrators may be able to better manage their apps with this explicit allocation.

B. Design & coding

The design of this software product, as shown in Figure 5 , mainly focuses on the procedure of receiving and exporting processed data. Simply put, the expected equation is the input data, which will be sent to the system for formatting and calculating, and then the system exports the output result for sending back to the user.

Figure 5 . AiMA system design.

This diagram is created to visualize the entire process of the system. The full process of how a user interacts with a system is shown in the diagram, along with how the system processes information and responds to the user. This makes the system expandable as well as easy to operate and maintain.

The client-server architecture is frequently applied to every mobile application, so this is not an exception for mathematics mobile systems. The main programming languages used in this system are JavaScript and Python.

Using JavaScript for mobile apps enables rapid development for the client side because it does not necessitate a sizable upfront investment or much work 12 . The most prominent is React Native 13 , a framework created to build clients for mobile applications. The purpose of React Native is to render the user interface and optimize the user experience. React Native takes on the primary responsibility of receiving user requests, specifically in this application, math problems, which can be an equation or a math operation. Regarding the back-end server, Flask, a Python server, is used for the implementation because of its benefits. It is server software that can handle HTTP requests on the public internet, private LANs, and private WANs 14 . This is a microweb server written in Python to execute numerical data from the client. Python is well known as an ideal programming language for the execution of math and data science aspects. Additionally, Python has powerful math libraries such as Numpy, Sympy, and Statistic. These libraries can perform complicated mathematical operations, including trigonometric, exponential, and logarithmic functions. Therefore, it works perfectly as a calculator server in a mobile math application.

In the input process, users can type in the edit box or scan by their mobile device’s camera to recognize the mathematics input equation. It is simple to manually type the InputField component or React Native to interact with the app’s client. For the AI scanner, the library react-native-image-picker supports picking and capturing the image via the device’s camera. However, the image is not sent directly to the server. An object containing URI, image type, and image name will be passed to the cloud-based platform Cloudinary for uploading. This process is performed when receiving a URL of Cloudinary, which must be followed by the form to ensure the accuracy of the system: ‘res.cloudinary.com/{cloud_name}/image/upload/ {public_id}.{format}'. As previously mentioned, the Axios library is integrated into this system for binding the client with the server via the HTTP request.

The process will start with the first option, which is using the keyboard for typing by the user . The input string after being passed to the Flask server for processing. If the input is valid, the system will check the attached baseURL received by Axios and send it to the corresponding back-end address for further processing actions. After receiving the correct string, the server side will use Regex, a string of letters that designates a text match pattern from Python for formatting the input equation. After that, the Flask server uses Sympy and NumPy, popular Python libraries for mathematical calculations. With the help of symbolic mathematics in both libraries, the server can conduct extended-differ operations, manipulate algebraic expressions, solve equations, and more. The extra library ‘statistics’ is imported for statistical calculations for the Probability and Statistics field. It provides functions used to process numerical data and calculate common statistical problems. Then, the server was able to export the output, which includes the result of the problem and the sequence of steps for rendering in the client view. The procedure will be quite different if the user uses the application's scanning feature. The input will be in image format. This work incorporates an AI model known as pix2tex. Pix2tex 15 stands for “picture to Latex," meaning that this model plays a role in converting images and text. For the model to recognize the image, several steps are required to process it.

• The Python Imaging Library (PIL) is used to image the class within it to display the image.

• Base64 is used for encoding and decoding the URL/URI of images.

• BytesIO is a class of Python that permits an object of IO data to be stored and executed in the byte format.

• Sympy: a powerful library that can handle the

First, a URL of Cloudinary will be used to send the captured image to the Flask server. Second, base64 is in charge of encoding the legitimate URL and decoding it for BytesIO's bytes-to-bytes translation. Finally, PIL reads the output, enabling the AI model to identify the input image. This pix2tex AI model aims to find a corresponding LaTeX code for a given image of an equation. An example of the Latex Math Code is shown in Figure 6 .

Figure 6 . An example of the latex math code 15 .

After receiving the string of Latex, the back-end system can be formatted by Regex for correctness and the Sympy library. This potent library can be used for latex string-based computations. One limitation of this model is that the ability to recognize handwriting has yet to be optimized. This will also be something that needs to be overcome in the future. The process ends when the client obtains the output as a latex string, which will be converted to mathematical characters for rendering on the user interface using the Mathview library.

The software product can be developed in the coding stage based on the previously created design documents. The development environment (Visual Studio Code), language programming (JavaScript, Python), or internet hosting service (GitHub) can be applied for implementation in the purpose actualization of the mathematics mobile application.

C. Testing & Deploy

For convenience, this application has been used in Android Studio, which is responsible for providing an emulated mobile device platform. However, the software must allow it to run on an actual device to reach the end user. Therefore, deploying the software on a mobile device to test the system's functionality is paramount.

To display the entire software on an actual device, connecting via WiFi is an effective and straightforward way:

• Running “gradlew assemble” in “android” inside React Native folder to export the apk file.

• Run this apk file on the mobile device.

• Go to Dev Settings → Debug the server host and port for the device to change the machine’s IP, which can be checked by “ipconfig” in the command box.

• On the server side, replace the current URL with this IP with port 8081.

• Reload the app.

• The software created in the earlier stage is verified to meet the functional requirements determined during the requirement collection and analysis stage.

Results

AiMA could satisfy some essential values after a portion of it was finished when it would be feasible to tackle the problems relating to simple mathematics operators, calculus, and numerical methods. Figure 6 shows a screenshot of AiMA.

Figure 7 . The screen shows the result and steps on a mobile device .

Figure 7 indicates the demonstration of AiMA when executing an optimization method problem, which is the golden section search. Instead of using standard mathematical techniques, such as multilevel derivatives, to determine the extreme point of the function, this search application uses an iterative method to find the answer. The user is required to provide the needed data. For instance, in this case study, this is a string of the function, the start and end values of a specified interval, the desired error, and finally choose the condition about the maximum or minimum requirements. The server consequently receives the request from the client. Because an iteration will be applied to solve this question, it can be considered between using a while-loop or for-loop. The while loop is appropriate because the number of iterations to be done is unknown in advance, and a condition check is required after each iteration. Furthermore, a computation in a while loop takes only two milliseconds to finish, whereas a calculation in a for-loop takes four milliseconds. For this reason, it is wise to utilize a while-loop to calculate the problems related to the iterative method. However, it will take longer for the user to obtain a response from the server. In this case study, the server's response time to the client was five milliseconds, including the execution time previously specified. Due to the server, the study was tested locally in this case. Network factors will cause the measurement time to increase when the server is deployed in a production environment. This is entirely controllable due to efficiency improvements for client-side rendering and execution time optimization. Furthermore, the accuracy is relatively high after using AiMA to compute this case study's problem. AiMA produces results with a 98% accuracy rate compared to verified hand calculations and is nearly flawless compared to trustworthy computing apps. Although the accuracy is imperfect, it is acceptable because the returned values are rounded rather than displayed in their entirety to provide the user with the most logical display. This mathematics mobile application is currently portable when deployed on an Android smartphone. In addition, specialized algorithms are constantly being updated, such as the golden section search method, Newton's method, Euler's method, Heun's method, and Simpson's rules. Not only do they return exact results, but the step-by-step box is also always displayed in detail and easily understood. Applying react hooks, such as useMemo and useCallback, which limit the amount of time the interface is rendered again, dramatically enhances performance. The comparisons among AiMA and related mobile systems are shown in Table 1 . Overall, AiMA has met most of the basic features of a math application. UI and UX are simple but intuitive, making it easier for users to interact with the system. To support the users in editing the input equation flexibly and accurately, and especially following the convention of mathematics form, the client side applied Mathquill. This library supports converting the string from the keyboards and mathematics symbols. However, this library cannot be integrated into this application because it cannot accommodate the mobile platform. Therefore, to overcome this limitation, Webview was applied. This is a React Native component that helps render the content on the native view. However, Webview only supports writing web pages in HTML, CSS, and vanilla JavaScript. This can lead to many limitations when there are some functions that vanilla JavaScript cannot replace and perform, such as how framework React can do. Nevertheless, it is an efficient way to achieve these essential functions.

The AI model integrated into the project performed well by reading image data and converting them to latex format. However, as mentioned above, the model has difficulty recognizing handwriting from the user, which means that it can only read typed symbols from the keyboard. One reason for this limitation is that the dataset could be better. In addition, this model only works well when the image's resolution is optimized, so when zooming in too much into the image, which can cause noise and image distortion, the model may also work incorrectly. Additionally, AiMA permits choosing photos from the gallery when scanning photos - something that a few other math apps on the app store need to look into. Users then have more options.

Table 1 Comparisons among AiMA and related mobile systems

Discussion, Conclusion, and Future Work

The value and influence of mathematics in people's lives are increasing as technology develops. Particularly in education, the rise of mobile technologies has brought about several advantages, including portability, ease, and accessibility. Creating a mobile system that can serve college and university students and high school kids is essential, providing answers to simple math problems and more advanced algorithms. The mathematics mobile applications published on the market generally offer various features with a high accuracy rate calculator system. Nevertheless, these software products are only designed to support mathematics topics for 12th-grade students and below, which means that the need for more advanced fields can limit the reachability to another group of customers, university students. In addition, despite the understanding that money is used for maintaining the application, from the perspective of someone who has experienced many mathematical applications, it is possible to realize the limitations of the free-package package of some applications, including Mathway. Hence, to create the best application and reach the end user, the consideration of creating a product that is priced, even for free, is worth considering.

To meet this requirement, this study introduces AiMA, a mobile AI-based system that helps college students with math-related problems. The client-server architecture is used to host, deliver, and manage the resources and services that the client requests. Aiming to build a software product, applying the development model—in this case, the waterfall methodology—is essential. This model is easy to manage due to its clean structure. In addition, the waterfall is the ideal software development model for small-scale software projects with specific requirements. The research mainly concentrates on specialized fields in mathematics, such as numerical methods in theoretical models in computing subjects and probability and statistics problems. AiMA offers substantial advantages over competing alternatives by enabling users to solve challenging calculus problems and obtain customized answers for specific mathematics topics, according to an evaluation of the system's capabilities. AiMA is an invaluable mobile system for college and university students needing specialized mathematics assistance.

For future work, the AI feature should be optimized. A few methods can be used to improve the AI system. The first is to be able to collect more data because the more data there are, the more accurate and efficient the AI model will be. In addition, cleaning and preprocessing the data to reduce noise, outliers, and inconsistencies is crucial before training the model. Techniques such as dimensionality reduction, feature scaling, and data standardization may be used. In addition, programming more specialized fields related to mathematics for the application: recognizing the complexity and variety of problems and diversifying solutions is a necessity. After the field of theoretical models in computing is completed, the field of probability will be the next area to be studied.

Abbreviations

UI: User interface

UX: User experience

AI: Artificial intelligence

HTTP: Hypertext Transfer Protocol

CNN: Convolutional neural network

RNN: Recurrent neural network

OCR: Optical character recognition

TMC: Theoretical models in computing

IT: Information technology

ODE: Ordinary differential equations

R&D: Research and development

ViT: Vision transformer

URL: Uniform resource locator

LANs: Local area networks

WANs: Wide area networks

URI: Uniform resource identifier

PIL: Python imaging library

IO: Input/output

IP: Internet protocol

Acknowledgement

We would like to extend our sincere gratitude and appreciation to the AIoT Lab VN for their invaluable support. Their assistance has been instrumental in our endeavors, and we are truly thankful for their partnership and collaboration.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Authors’ contribution

Conceptualization, T.D.L., N.A.D.N.; Data curation, N.A.D.N.; Methodology, T.D.L., N.A.D.N.; Project administration, T.D.L.; Software, N.A.D.N.; Writing–original draft, T.D.L., N.A.D.N.; Writing–review and editing, T.D.L., N.A.D.N, K.D.D.N, B.N.L.N. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

We have no conflicts of interest to disclose.