Sensitivity of secondary particle emission to hadronic physics models in GATE/Geant4 proton therapy simulations at 100 MeV

Abstract

Introduction: Proton therapy simulations rely on Monte Carlo techniques, such as the GATE code based on the Geant4 toolkit, to predict dose distribution and secondary particle production. The accuracy of these simulations is heavily influenced by the chosen physics models.

Methods: In this study, we analyzed three Geant4 hadronic physics models, BIC, BERT, and INCL++, by calculating the angular and energy distributions of secondary neutrons and gamma particles. We conducted GATE/Geant4 simulations on a water phantom irradiated with a 100 MeV proton beam.

Results: Our investigation revealed notable differences in the angular and energy distributions of emitted particles among the three models.

Conclusion: This study emphasizes the necessity of carefully selecting a hadronic physics model for GATE/Geant4 simulations in proton therapy.

INTRODUCTION

In the last decade, proton therapy has garnered increasing interest for cancer treatment due to its potential to significantly reduce dose exposure to healthy tissues while effectively targeting cancer tissue 1 . Monte Carlo transport simulation codes, such as FLUKA and Geant4, are commonly used to simulate particle transport and interaction processes in proton therapy 2 . These codes enable calculations of dose distributions in patients or simulated phantoms, which are vital for treatment planning. Therapeutic proton beams often generate a substantial amount of secondary particles, which significantly contribute to fluences and the actual delivered dose. Accurate simulation of these secondary particles in a realistic proton therapy setup is crucial for two main reasons: secondary neutrons may pose a possible risk of developing secondary cancer 3 , and precise prediction of nuclear particle interactions and residual nuclei distributions is required for imaging and range verification techniques 4 using prompt gammas 5 .

Monte Carlo simulation serves as a useful tool for predicting proton beam properties in tissue. However, it has been pointed out that selecting the right physics models is essential for accurate predictions 2 , 6 . This work focuses on the GATE platform 7 , 8 , 9 , which is based on the Geant4 toolkit 10 , 11 widely employed in numerous proton therapy studies 2 , 3 , 4 , 5 , 6 . In the Geant4 simulation at therapeutic energies, the main processes are governed by a hadronic physics model of the intranuclear cascade (INC) type. Three different INC models included in Geant4 are the binary cascade (BIC) 12 , the Bertini cascade (BERT) 13 , and the Liège intranuclear cascade (INCL++) 14 . While these models have been shown to produce marginally different results for the primary dose 15 , the differences between these models in the predicted angular distribution and energy spectrum of emitted secondary gamma and neutron radiation in proton therapy setups have not been extensively investigated. These properties are crucial for range verification techniques using secondary gamma rays 4 , 5 and assessing the hazards posed by stray neutrons 2 , 3 . A significant challenge in choosing a suitable hadronic model lies in the scarcity of experimental data.

In this paper, we investigate the angular and energy distribution of secondary neutrons and gamma particles using three widely used Geant4 hadronic models, BIC, BERT, and INCL++. Our calculations involve a proton energy of 100 MeV irradiated on a cylindrical water phantom. We evaluate the hadronic model differences in the predicted result with a focus on the range verification and secondary neutron production aspects of proton therapy. This research will provide valuable insight into the suitability of these models for practical proton therapy settings. It also points out the specific configuration of experimental data necessary to determine and constrain the most appropriate physics model for Monte Carlo simulations in proton therapy.

METHODS

In this study, we use GATE version 9.1, which incorporates Geant4 10.7. The simulation setup employed in this study comprised a proton beam of 100 MeV directed at a cylindrical water phantom with a 10 cm radius and 11.58 cm length. The number of generated incoming protons is 10 million. The center of the water phantom was positioned 50 cm away from the source along the z-axis. A PhaseSpace Actor directly attached to the water phantom was utilized to collect and process the physics information of particles entering or generated within a specified volume, such as particle name, energy, interaction position (x, y, z), particle direction (dx, dy, dz), interaction process, and mass of produced particles. The output data are stored in root format.

The Geant4 toolkit underlying the GATE framework offers the flexibility to select from a variety of physics models to optimize their application in different contexts. To depict proton interaction processes with matter, physics models covering all energy ranges are necessary. At high energies at the GeV scale and above, Geant4 provides the Quark-Gluon String (QGS) 16 , 17 and the Fritiof-like String (FTF) 18 models. For proton therapy energy ranges, Geant4 employs the Bertini Intranuclear Cascade (BERT) 13 , Binary Cascade (BIC) 12 , and Liège Intranuclear Cascade (INCL++) [14] models, which are the models examined in this study. Additional models include the Precompound and evaporation models 19 for de-exciting the residual nuclear particles after high initial energy interactions, the Electromagnetic (EM) packages 20 for describing electromagnetic interaction processes from 0 to 100 TeV, and the High Precision neutron model (HP) 21 for neutron-induced interactions below 20 MeV.

The considered proton-induced nuclear reaction processes were simulated by applying the chosen models to various reaction processes over time. Separate models were required to address the intranuclear cascade process, the preequilibrium state of the nucleus, and the de-excitation process of the equilibrated nuclear state. To simulate the cascade stage within the proton energy range used in therapy, Geant4 offers three models: BIC, BERT, and INCL++. The selected hadronic physics models for simulation and comparison included BIC (QGSP_BIC_HP_EMY), BERT (QGSP_BERT_HP_EMY), and INCL++ (QGSP_INCLXX_HP_EMY). Here, we give a brief description of some main physics assumptions of the three models.

The BERT model comprises three successively connected components: intranuclear cascade, preequilibrium, and simple evaporation models. The target nucleus in the BERT model is presented in Woods-Saxon form approximated by several concentric shells (up to six shells) of constant density. The BERT intranuclear cascade model is based on Bertini’s idea of solving a Boltzmann equation using the Monte Carlo method 13 with straight-line propagation. After the intranuclear cascade phase, the preequilibrium phase is modeled by the Griffin exciton model 22 , where smaller particles are emitted until the excitation energy of the remnant reaches a threshold. The nucleus is further de-excited as described by a statistical Weisskopf model 23 and Fermi breakup by emitting light particles followed by a continuous gamma emission chain in the end. Compared to the BIC and INCL++, several simplified approximations have been made in the BERT model to reduce its calculation time, which is required for applications in the GeV-scale energy region.

The BIC model 12 also included three separate models for the intranuclear cascade, preequilibrium, and evaporation models. However, it is noted that the descriptions for these three stages of BIC are very different from those in BERT mentioned above. In the binary collision intranuclear cascade model of BICs, the participating nucleons are considered Gaussian waves with defined positions and momenta at a specific time. These nucleons are propagated in curved trajectories according to an equation of motion with a simple time-independent potential. The target nucleus in this stage uses either a Woods-Saxon or harmonic-oscillator shape for the nucleon density. For the precompound stage, BIC uses the native Geant4 preequilibrium model, which is a semiclassical exciton model 19 . Finally, the de-excitation state is described by the native Geant4 de-excitation model, where a combination of tabulated discrete states and parametrized continuous distribution is used for photon evaporation (i.e., gamma emission) 19 .

In the Liège INCL++ model 14 , the particles propagate in straight-line trajectories in static potential, where the model keeps track of varying time steps of all participating particles. The target nucleus has a Woods-Saxon density. Unlike the BIC and BERT models, there is no explicit precompound model used in INCL++. At the end of the cascade phase, the emissions of particles and photons from the remnant nucleus are described by the native Geant4 de-excitation model 19 , which is the same as the one used in the BIC model.

RESULTS

In this part, we assess the total production, as well as the angular and energy distributions of secondary neutron and gamma particles within each hadronic physics model. A direct comparison is carried out between three cascade models, specifically BERT, BIC, and INCL++. The proton depth dose of several Geant4 models has been studied before, and no strong discrepancies have been reported 24 , 25 therefore, we do not perform calculations for these quantities in this work.

All calculations in this work are performed on a single core of a CPU with clock speeds ranging from 1.7 GHz-2.7 GHz. The production set cut value in the water phantom is 0.1 mm. The times needed to simulate 10 ⁷ protons at 100 MeV using this configuration for the three different hadronic models are listed in Table 1 , along with the total amount of secondary neutrons and gammas.

Table 1 Numbers of secondary neutrons and gamma rays produced in the water phantom along with their computational times.

Figure 1 . Energy spectrum of secondary neutrons on a linear scale.

Figure 1 and Figure 2 show the energy spectra of the secondary neutrons calculated by the three hadronic models on linear and log y-axis scales, respectively. All three models generate neutron energy spectra up to 90 MeV. Most neutrons are produced in the energy range of 1-6 MeV.

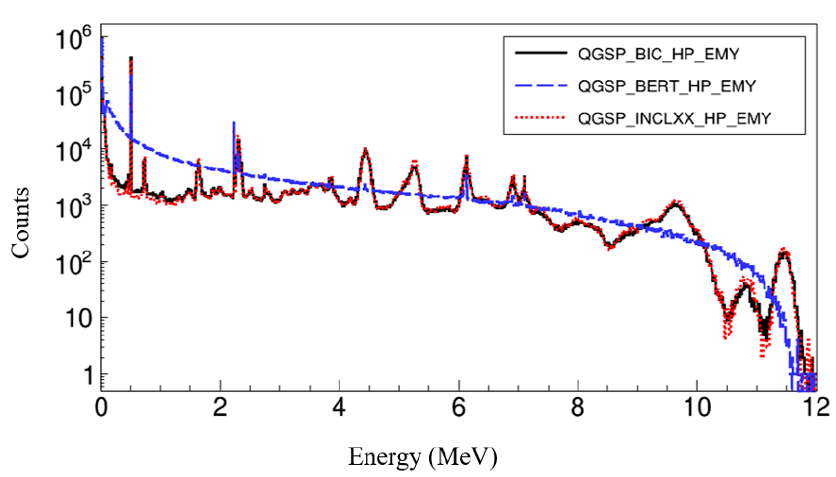
Figure 2 . Energy spectrum of secondary neutrons in log scale.

Figure 3 . Angular distribution of secondary neutrons.

Figure 3 presents the angular distributions of the secondary neutrons generated by the three cascade models. The angular distribution is calculated based on the 3D momentum vectors of the neutron recorded in the Geant4 simulation. The angle θ is defined as the lab-frame scattering angle of the secondary neutron with respect to the incoming direction of the proton. The distribution of particles scattered in the azimuthal angle ϕ is isotropic and therefore is not shown here.

Figure 4 . Energy spectrum of secondary gammas in log scale.

Figure 4 presents the energy spectrum of secondary (prompt) gamma generated from the three hadronic models. The pronounced peaks seen in the BIC and INCL++ models are from the pair annihilation, deuteron formation, and de-excitation processes of fragment excited states.

Figure 5 . Angular distribution of secondary gammas.

Figure 5 presents the angular distributions of the secondary gammas generated by the three cascade models. The gammas are emitted in a slightly forward direction due to the kinematics of the moving excited fragments. The azimuthal angle is isotropic, similar to the neutron case.

DISCUSSION

Table 1 shows that proton bombardment of a water phantom generates a significant number of secondary neutrons and gammas in all three models. The secondary particles account for 3.5%-4.7% and 22%-32% of the incoming protons for neutrons and gammas, respectively. All of these secondary particles originate from the reaction between the incoming proton and the ¹⁶ O nucleus in the water phantom. The probability of secondary neutron production differs among the three models, with the BIC model producing the most neutrons and the BERT model producing the most gammas. The difference in the produced particles between the models can be up to 34% for the neutron case and 45% for the gamma case. Such a large discrepancy can affect the dose calculation of these particles. We note that due to the simplified approximations used in the BERT model compared to the others, it is approximately 20% faster to calculate the specific scenario studied in this work using BERT versus BIC and INCL++. However, these approximations will unavoidably affect the simulation results, as we can see in Table 1 and Figure 1 - Figure 5 .

Figure 1 , Figure 2 indicate that the BIC and INCL++ models have rather similar neutron energy spectra, while the BERT model focuses more on the low-energy region. The similarities between the BIC and INCL++ models are also applied to the angular distributions in Figure 3 , while the BERT model yields fewer particles in the forward angles compared to the other two models. The differences in the simulated neutron energy spectrum at energies of approximately 40-50 MeV and angular distribution at angles below 45 degrees between the three main hadronic models in Geant4 mainly come from the cascade stage, where the models have drastically different assumptions and descriptions of this process, as presented in the methods section. The very good agreement between BIC and INCL++ results at energies below 10 MeV is because of the implementation of the same native Geant4 de-excitation, which is more sophisticated compared to the one used in BERT. The simple de-excitation is also the reason for the more isotropic neutron angular distribution of BERT compared to the others. These generally different results suggest that the prediction based on the simulation results from these models for the secondary neutron, which is important for secondary cancer estimation and neutron shielding calculation, could contain large uncertainty and should be taken with great precautions. Our calculations suggest that more direct experimental measurements of neutron angular distribution with a water phantom or ¹⁶ O target in the proton therapy energy region are needed to identify the most suitable hadronic models.

In Figure 4 , the gamma peaks of the energy spectrum from the BERT model have a rather smooth shape with very few peaks. This is in stark contrast with the energy spectra of the BIC and INCL++ models, which contain many peaks and are almost identical to each other. Again, this is because the INCL++ and BIC models share the default de-excitation model of Geant4 in the final stage of the reaction chain 19 , 14 , 12 , which explicitly includes the tabulated data for several discrete excited states, whereas BERT uses a faster but simpler de-excitation model 13 , which can only simulate the continuous gamma spectrum. Given the existence of the known excited states of the fragments in the p + ¹⁶ O reaction, the simulated spectra of BIC and INCL++ are clearly more accurate than that of BERT. We note that some fine peaks produced by the BERT models are due to the additional coupling to the High Precision neutron model, which all three models use for low-energy neutron reactions.

For the angular distribution in Figure 5 , the three models have identical shapes but different amplitudes due to the difference in the number of produced gammas. The uncertainty in the prompt gamma spectrum and total gamma number prediction will greatly affect the range verification methods of proton therapy using prompt gamma. Similar to the neutron case, more data for prompt gamma energy spectra are needed to identify any limitations in the hadronic models and improve them.

CONCLUSION

In this work, we investigate the secondary neutrons and gammas generated from a water phantom bombarded with a 100 MeV proton beam using three different hadronic models in Geant4 simulations, namely, the BIC, BERT, and INCL++. Throughout the study, several issues were addressed. The energy spectra and angular distributions of the secondary neutrons and gammas generated by these models were analyzed and evaluated. The neutron energy spectra and angular distributions in all three models are different compared to each other. The gamma angular distributions are mostly isotropic and have the same shape in all three models. The BIC and INCL++ models have similar gamma energy spectra that are more accurate than that of BERT.

Our study revealed significant differences among the three physical models used in Geant4 to describe the process of proton beam therapy. However, there is currently too little experimental data to determine which model is the most accurate. Based on the results of this study, appropriate experimental measurements are encouraged to be conducted to determine or create the most suitable model for proton beam therapy.

LIST OF ABBREVIATIONS

BERT: Bertini cascade

BIC: binary cascade

GATE: Geant4 Application for Emission Tomography

INC: intranuclear cascade

INCL++: Liège intranuclear cascade

COMPETING INTERESTS

The authors declare that they have no conflicts of interest.

ACKNOWLEDGEMENTS

This work was funded by Vietnam National University, Ho Chi Minh City under Grant number B2022-18-01.

AUTHORS’ CONTRIBUTIONS

Pham Thi Cam Lai performed the calculations. Nguyen Tri Toan Phuc and Vo Hong Hai discussed the results and prepared the manuscript.