Open Access 
Abstract
The wire arc additive manufacturing (WAAM) process involves a multitude of uncertain parameters, making WAAM a complex system for analysis. To comprehensively investigate their effects and conduct sensitivity studies, a parametric approach is essential. However, such an approach necessitates a substantial number of simulations, each of which is time-consuming and can last up to a few days. In response, we construct a deep learning-based surrogate model trained on the data created by the validated finite element (FE) method. This surrogate model is used to conduct sensitivity analysis via the SHapley Additive exPlanations (SHAP) method. The findings indicate that the positioning of the laser and its proximity to individual nodal points during the printing process are crucial features in predicting temperature evolution. Additionally, using the FFNN model instead of solely the FE model significantly reduces the computational cost (3272 times) of predicting the temperature field. This innovative approach promises to streamline the exploration of the intricate parameter space of WAAM, offering valuable insights for enhanced process optimization and control of complex manufacturing processes.
Introduction
In the realm of additive manufacturing (AM) processes, wire and arc additive manufacturing (WAAM) stands out as a versatile method capable of producing large parts with moderate shape complexity and commendable dimensional accuracy 1 . This technique boasts distinct advantages over other manufacturing processes, primarily characterized by its high deposition rate and cost-effectiveness in terms of equipment investment 2 , 3 . However, the WAAM method introduces many inherent drawbacks resulting from complex thermal evolution, high heat accumulation, low dimensional accuracy, and poor surface quality 4 , 5 . Therefore, it is essential to perform a thorough sensitivity analysis that quantifies the variation in the input process parameters on the final printed quality.
Currently, thermal analysis during the WAAM process can be conducted using the high-fidelity finite element (FE) method 6 , 7 , 8 or by analyzing thermal signals acquired by thermal sensors, such as thermocouples 9 , pyrometers 10 , and IR cameras 11 . In addition, achieving high-quality printed products and ensuring optimal manufacturing conditions involve dealing with various sources of uncertainty 12 , 13 . These encompass factors such as material properties, operator expertise, process parameters, and boundary conditions 14 . Gaining a comprehensive understanding of these uncertainties typically requires a series of experiments or FE simulations, which can be both time-consuming and costly, often taking up to several days 14 , 15 . This challenge has significantly reduced the widespread adoption of WAAM in industry 16 .
One effective solution to this problem is to develop a surrogate model through machine learning (ML) techniques 17 , 18 , 19 . Such a model enables swift and precise predictions of product quality. For instance, prior studies by Mozaffar et al. 20 and Pham et al. 21 have successfully built surrogate models for predicting thermal histories in directed energy deposition (DED) processes, employing recurrent neural networks (RNNs) and artificial neural networks (ANNs), respectively. Similarly, Roy et al. 22 proposed an ANN-based surrogate model for predicting temperature evolution in fused filament fabrication (FFF) processes. However, it is worth noting that these studies primarily focused on the DED process. To the best of the author's knowledge, the application of ML-based surrogate models to WAAM is still in its early stages 2 , 3 . Furthermore, some of these previous works utilized complex models such as RNNs and lacked interpretability of the ML model. Hence, we developed an explainable ML-based surrogate model that aims to capture the relationships between input parameters and temperature evolution efficiently and accurately.
To further illustrate our ML model, we conducted an extensive sensitivity analysis (SA) 23 , 24 . This SA aims to provide deeper insights into the underlying physics of the WAAM process, further enhancing our understanding and potential for optimization. However, relying solely on ML methods for SA proves inefficient, as ML-based models often function as black boxes 25 . Figure 1 illustrates the workflow employing the ML-based surrogate model as a black box for predicting temperature fields in the WAAM process. The input parameters is learned by the ML-based model as a blackbox to predict temperature fields. While these models offer computational efficiency, their effectiveness is constrained by their lack of debuggability and the inability to provide human-understandable and reconstructable explanations for the predicted temperature fields. Additionally, it is not possible to obtain insights into the models' internal working, i.e., how and why temperature fields are predicted 26 . The current workflow's lack of reactivity restricts its applicability in real-time settings, a critical requirement in industries where thorough model verification and validation are essential 27 .
Figure 1 . The workflow employing the ML-based surrogate model as a black box for predicting temperature fields in the WAAM process.
To address these issues, explainable ML research topics have recently been developed 28 , 29 . The explainable ML techniques provide meaningful insights into the impact of selected input features on the output target feature 30 . Figure 2 shows the workflow using the surrogate model and explainable ML techniques in the WAAM process. The ML-based model is interpreted by the explainable model to clarify better for the process. Compared to Figure 1 , the black box of the ML-based model is now “open”. Owing to explainable ML techniques, the prediction of temperature fields produced from an ML-based model, i.e., the peaks and cyclic behaviors of temperature evolution, is understandable.
Figure 2 . The workflow using the surrogate model and explainable ML techniques in the WAAM process.
Drawing upon these contextual foundations, this article aims to perform an SA on the WAAM process using an explainable ML model. This study is organized as follows: the FE model of WAAM is summarized in Section 2. The ML-based surrogate model and explainable ML techniques are described in Section 3. In Section 4, the numerical results of the FE and ML models are discussed. Finally, the sensitivity analysis and discussion are presented in Section 5 prior to the conclusion.
Finite element model for the WAAM process
Geometry and thermophysical properties of the WAAM wall
Figure 3 (a) shows the baseplate geometry in this study, which is 200 mm in length, 80 mm in width, and 10 mm thick, and its corresponding 3D model geometry. In this study, only the thermal problem was studied. Stainless steel 316 L stainless steel (SS 316 L) was used for both the wall and baseplate materials, and the thermophysical properties were chosen for the numerical simulation, as described in 2 , 3 . As shown in Figure 3 (a), the path of the laser encompasses both forward and reverse layers, with one track per layer. This parameter significantly influences the resulting microstructure and mechanical properties of the additive manufactured part 31 .
Figure 3 . Geometry of the 3D WAAM model, (a) trajectory of the 3D model and (b) 3D view of the geometry.
The 3D model, depicted in Figure 3 (b), features a six-layered structure specifically designed for this study. To capture areas with high thermal gradients, a refined mesh with dimensions of 0.8x0.1x0.1 mm³ was implemented in three regions: the clad and its immediate vicinities on the substrate. With increasing distance to the deposition path, the element size coarsened toward the edges of the specimen. Based on a convergence study, this mesh size can be evaluated as sufficient, which is consistent with the result reported in 31 . As one moves further from the deposition path, the element size gradually increases toward the specimen's edges. A convergence study validated this mesh size as adequate, aligning with findings presented in 31 . Additionally, to develop the FE model for thermal simulation, the thermophysical properties of SS316L reported in 31 and Goldak’s heat source model ( Figure 4 ) were chosen for the numerical simulations.
In this study, we assumed identical thermophysical properties for both the base plate and the thin wall, despite their differing microstructures. Additionally, we understand that the entire process, including the behavior of the wall geometry, is of paramount importance. While this assumption may appear simplified, it aligns with previous studies in the field 31 . Nevertheless, it is important to note that this assumption may introduce certain simplifications in the model. Future work could explore the implications of considering distinct thermophysical properties for base plates and thin walls, which may lead to a more comprehensive understanding of the process.
Heat input modeling
A Goldak volume heat source 32 based on double ellipsoidal power density distributions was used in this study. Figure 4 illustrates the heat distribution of a double ellipsoidal heat source model. The heat flux is modeled in Z-direction with its parameters were selected as those in 32 : a f = 7 mm,a r = 13 mm, b = 4 mm, c =4 mm,f f = 0.6, and f r = 1.4.
The WAAM process simulation was performed using ANSYS software. Before the simulation, all the clad layers are considered inactive (dead) elements since they do not exist before the WAAM process (phase prestep). During the process, the dead elements are reactivated successively under the effect of the welding torch using an activation time that was modeled through the welding speed. This method suffers from a computational time disadvantage, but it can help to model the process in practice accurately.
In general, the temperature evolution can be predicted as
where q = [x, y, z, t, m i ] is a multidimensional vector of the spatial coordinates (x,y,z), the time (t), and the other input parameters (m i ), i.e., the current intensity. As discussed in the introduction section, solving the above equation is time-consuming, i.e., six hours for one simulation. As a result, we constructed an ML-based surrogate model to reduce computational costs. The following section introduces the specific ML-based surrogate models employed in this study.
Sensitivity analysis using explainable ML for the WAAM process
In this section, we introduce the SA using the explainable ML method, constructed using the outcomes derived from the FE model. The FE model is responsible for calculating the temperature variations within the WAAM process under various input heat energy conditions. Additionally, we incorporate an ML-based explainability method to further elucidate the surrogate model's decision-making process.
ML-based surrogate model
Model selection
Several algorithms, including linear regression, random forest, and feedforward neural networks (FFNNs), can be used to construct ML-based surrogate models. In this study, we choose the FFNN architecture owing to its ability to approximate highly nonlinear relationships within the physics of WAAM. Moreover, the FFNN will be expanded to incorporate an explainable method, thereby enhancing the interpretability of the sensitivity analysis.
Data collection
The training data for the ML model are generated through simulations using the FE model outlined in Sec. 2. These simulations consist of various values of key WAAM process parameters, namely, the current intensity ( I ) and velocity ( U ). The resulting training dataset includes four distinct simulations, detailed in Table 1 . Each of these FE simulations results in a temperature field corresponding to a specific combination of U and I .
In each FE simulation, we accumulate a substantial dataset, with a total of 19,126,800 data points (10626 nodes × 1800 timesteps = 19,126,800) for a given pair of U and I. As demonstrated in Table 1 , we employ four FE simulations with {I, U} = {120, 0.2}, {126, 0.3}, {138, 0.5}, and {144, 0.6} to train the ML model, yielding approximately 76,507,200 data points. These training datasets are subsequently partitioned into two sets, one for training and the other for validation, allowing for fine-tuning of the ML model's performance.
To assess the predictive accuracy, we subject the ML model to an unseen FE simulation for {I, U} = {132, 0.4} as our testing dataset. This evaluation ensures the robustness and reliability of our model's prediction capabilities.
In addition to improving the prediction accuracy of the model, we added four additional features, namely, the heat source position x a , z a and the distance from the heat source to the FE nodes d x , d z . Note that these features are chosen by the trial-and-error approach. To avoid adding substantial length to the paper, the overall description of these features and the feature selection process can be found in 6 .
In general, the ML model can be represented as
where W is the weight and q is the input, which includes the spatial coordinates (x, y, z), the time (t), the current intensity (I), the velocity (U), the heat source position , and the distance from the heat source to the FE nodes (d x , d z ). The output is the temperature at each spatial coordinate at a specific time.
Explainable ML method
To provide a deeper understanding of the predictive capability of the FFNN-based surrogate model g, we subsequently describe the explanatory ability of the FFNN-based model. In this work, the SHAP method 33 , 34 is used to explain the FFNN-based surrogate model. The SHAP method was developed based on Shapley from cooperative game theory 35 .
Let N be the set of all input features of the FFNN g, and S denotes a subset of N. The SHAP value assigns a value ϕ i (q), with i = 1,2,…,n, to each feature representing this feature's contribution to the model prediction. This value is computed as
where |N| is the number of features in the set N and |S| is the number of features in the set S. However, the SHAP method requires training the model g q for all subsets S ⊆ N and thus significantly increases the computational cost. Additionally, most of the ML-based models do not accept arbitrary patterns of missing input. Therefore, the SHAP method was developed to overcome these problems. In particular, the SHAP method proposed an approximation based on conditional expectation as
where q S and z S are |S|-dimensional vectors that collect values of the features in S from vectors q and z, respectively. As a consequence, the missing features q i in Eq. (1) can be randomly drawn from the background data (normally the mean value) to obtain an approximation for g q (S). Therefore, the SHAP method significantly decreases the computational cost compared with the original Shapley method. The SHAP method ranks the importance of features on the task performance of the ML model.
Results
This section presents the results, including the FE results in Sec. 4.1 and the FFNN-based surrogate model results in Sec. 4.2.
Finite element results
Figure 5 depicts the temperature evolution at the middle point of the first layer in the clad, as obtained from the finite element (FE) model in this study. The temperature shows an oscillation behavior named as temperature oscillations that strongly influences the final microstructure. Additionally, after six thermal cycles, the temperature peak exhibits a progressive decrease. This can be attributed to the phenomenon of heat accumulation during the wire and arc additive manufacturing (WAAM) process. It is noteworthy that the number of temperature peaks in the thermal cycle corresponds to the number of layers deposited in the clad. Note that our ongoing experiments are aimed at validating the results obtained from the finite element model. Additionally, we would like to acknowledge that, in the FE simulation, we treated the wall height as a constant, and this can be considered an assumption. It is important to consider how altering the current intensity or laser velocity often leads to variations in wall height. Thus, we will consider this assumption in our future study.
Figure 5 . Temperature evolution predicted by the FE model for the middle point of the first layer in the clad.
Machine learning-based surrogate model results
This section presents the results of the temperature field prediction by the FFNN-based surrogate model, as discussed in Sec. 3.
Figure 6 . Three points are selected to represent the thermal cycle predicted by the surrogate model.
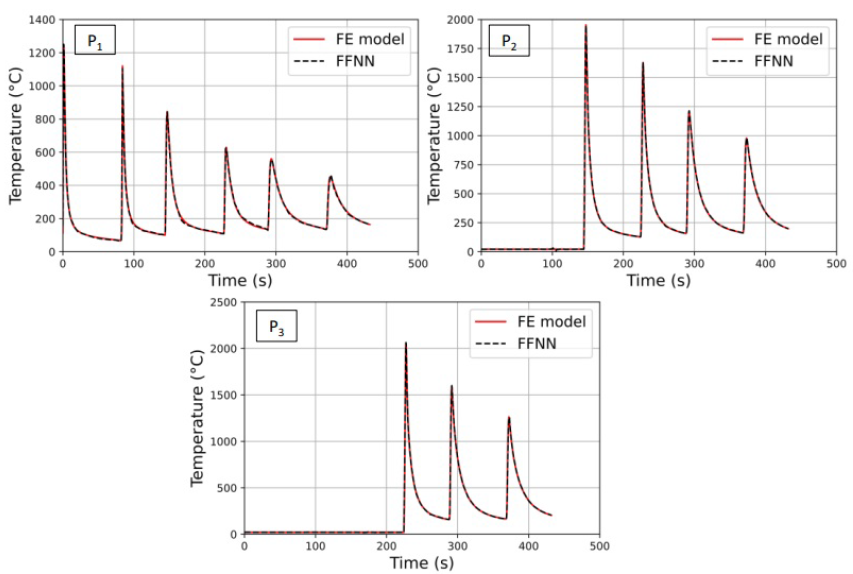
For ease of visualization, we selected three specific points to showcase the temperature evolution. These points are situated in the middle of the first, second, and third layers in the clad, denoted as P1, P2, and P3, respectively, as depicted in Figure 6 . It is worth noting that these points are anticipated to demonstrate the most intricate thermal cycles during the WAAM process, characterized by high-temperature peaks followed by gradual cooling cycles, as illustrated in Figure 5 . Furthermore, these points were extracted from a distinct test dataset that the model had never encountered during its training and validation phases.
Figure 7 . Comparison of the thermal cycles predicted by the FE model and the FFNN-based surrogate model for 3 points P1, P2, and P3.
Figure 7 displays the temperature evolutions derived from both the FE model and the FFNN-based surrogate models for three specified points, namely, P1, P2, and P3. The FFNN-based surrogate model accurately captures the thermal cycles at these points, reproducing both the temperature peaks and the subsequent cooling phases. Specifically, the R 2 values 36 , 37 calculated for these three points exceeded 0.99.
In essence, the FFNN-based surrogate model demonstrates good accuracy in predicting temperature evolution. The subsequent section will discuss the explanation of the FFNN-based surrogate model, employing the SHAP method discussed in Sec. 3. Hereafter, we carry out the discussion section to determine the physics inside WAAM using the ML explainable method.
Discussion
In this section, the sensitivity of the process parameters to the WAAM process is discussed, and the ML-based model is explained using the SHAP method.
Sensitivity analysis of the process parameters
The sensitivity analysis of the temperature evolution in response to variations in the current intensity and velocity is depicted in Figure 8 . As anticipated, increasing the current intensity facilitates more efficient heat propagation within the printed component, augmenting the energy delivered to the laser and consequently elevating the temperature. Conversely, a reduction in velocity leads to an increase in temperature. This phenomenon can be attributed to the fact that higher scanning speeds entail reduced time spent by the laser at any specific point on the powder bed. Consequently, the energy transferred to the material diminishes, resulting in lower temperatures compared to those of the case with slower scanning speeds.
Figure 8 . Sensitivity of the (a) current intensity I and (b) velocity U to the temperature evolution at point P1.
Sensitivity analysis of the ML-based surrogate model
Figure 9 shows the 95% quantile SHAP values corresponding to each feature. The absolute SHAP value is a measure of the feature contribution to the difference between the predicted temperature and its average value. Note that the 95% quantile is chosen since it is a standard evaluation criterion in statistics. As observed in Figure 9 , ,and constitute the most influential additional features for temperature prediction. In contrast, other features, such as x, y, z, t, U, and I, play a minor role in temperature prediction. Note that these features are basic features; therefore, they should not be translated as negligible parameters.
Using the SHAP analysis information in Figure 9 , this section introduces one base and four reduced FFNN-based models, resulting in five models to verify the ranking of the feature importance for temperature prediction and to determine the relevant features contributing to the temperature evolution behavior. The base model consists of only six basic features. The five consecutive reduced FFNN-based models are built by adding each feature in the order of their 95% quantile SHAP values. The description and R 2 values of the five FFNN-based models are included in Table 2 .
As listed in Table 2 , the base model poorly predicts the temperature fields, with a low R2 value of 0.7211. In addition, the R 2 values of each reduced model increase gradually with the addition of each feature. The R 2 value of the FFNN-based model reached 0.9964 for all the features. This result confirms that d z plays a vital role in temperature prediction.
Computational cost assessment
Table 3 illustrates the computational cost incurred when employing both the FFNN-based and FE models for temperature field prediction. As depicted, the FFNN-based model achieves this task in approximately 20 seconds, a substantial reduction of 3272 times compared to that of the FE model, which requires 18 hours. In summary, utilizing the FFNN model significantly speeds up the optimization and uncertainty quantification process, especially when thousands to millions of temperature field predictions for varying process parameters are needed.
Conclusion
In this study, we developed an interpretable machine learning model capable of quickly and accurately predicting the temperature field during the WAAM process. This model was trained using data generated from validated FE simulations. The key contributions of this research include the following:
The model shows a high R 2 value of 0.99 for predicting the temperature history. Moreover, its implementation substantially reduces computational costs from 18 hours to approximately 0.0055 hours.
Instead of adopting a conventional black-box machine learning model, we employed the SHAP method to enhance its interpretability, providing invaluable insights into the underlying processes.
A comprehensive sensitivity analysis was performed to determine the fundamental physics of WAAM. This result can lead to subsequent analyses, including optimization strategies and uncertainty quantification.
In perspective, we will develop an optimization framework that accounts for uncertainties, with the ultimate goal of producing high-quality WAAM products based on the findings of this study.
Acknowledgment
This research is funded by Thu Dau Mot University, Binh Duong Province, Vietnam, under grant number NNC. 21.2.012.
Author contributions
Thinh Quy Duc Pham contributes to the development of relevant theories, executes machine learning models, and authors articles.
Manh Cuong Bui contributes to perform the numerical simulation.
Thao Van Le, Bui Sy Vuong, and Xuan Van Tran contribute to paper revisions and provide feedback.
Abbreviations
AM: Additive Manufacturing
WAAM: Wire Arc Additive Manufacturing
FE: Finite Element
ML: Machine Learning
DED: Directed Energy Deposition
RNN: Recurrent Neural Network
FFF: Fused Filament Fabrication
SA: Sensitivity Analysis
SS: Stainless Steel
Competing interests
The authors declare no competing interests.
References
- Jafari D, Vaneker THJ, Gibson I. Wire and arc additive manufacturing: opportunities and challenges to control the quality and accuracy of manufactured parts. Mater Des. April 2021;202:109471. . ;:. Google Scholar
- Le VT, Bui MC, Pham TQD, Tran HS, Van Tran X. Efficient prediction of thermal history in wire and arc additive manufacturing combining machine learning and numerical simulation. Int J Adv Manuf Technol. 2023;126(9-10):4651-63. . ;:. Google Scholar
- Le VT, Nguyen HD, Bui MC, Pham TQD, Le HT, Tran VX, et al. Rapid and accurate prediction of temperature evolution in wire plus arc additive manufacturing using feedforward neural network. Manuf Lett. 2022;32:28-31. . ;:. Google Scholar
- Cunningham CR, Flynn JM, Shokrani A, Dhokia V, Newman ST. Invited review article: strategies and processes for high quality wire arc additive manufacturing. Addit Manuf. August 2018;22(June):672-86. . ;:. Google Scholar
- Jafari D, Vaneker THJ, Gibson I. Wire and arc additive manufacturing: opportunities and challenges to control the quality and accuracy of manufactured parts. Mater Des. January 2021;202:109471. . ;:. Google Scholar
- Lei Y, Xiong J, Li R. Effect of inter layer idle time on thermal behavior for multilayer singlepass thin-walled parts in GMAW-based additive manufacturing. Int J Adv Manuf Technol. 2018;96(1-4):1355-65. . ;:. Google Scholar
- Wang J, Lin X, Li J, Hu Y, Zhou Y, Wang C et al. Effects of deposition strategies on macro/microstructure and mechanical properties of wire and arc additive manufactured Ti-6Al-4 V. Mater Sci Eng A. 2019;754(November) 2018:735-49. . ;:. Google Scholar
- Montevecchi F, Venturini G, Grossi N, Scippa A, Campatelli G. Heat accumulation prevention in Wire-Arc-Additive-Manufacturing using air jet impingement. Manuf Lett. 2018;17:14-8. . ;:. Google Scholar
- Hackenhaar W, Mazzaferro JAE, Montevecchi F, Campatelli G. An experimental numerical study of active cooling in wire arc additive manufacturing. J Manuf Processes. 2020;52(January):58-65. . ;:. Google Scholar
- Takagi H, Sasahara H, Abe T, Sannomiya H, Nishiyama S, Ohta S et al. Material-property evaluation of magnesium alloys fabricated using wire-and-arc-based additive manufacturing. Addit Manuf. 2018;24(October):498-507. . ;:. Google Scholar
- Yang D, Wang G, Zhang G. Thermal analysis for single-pass multilayer GMAW based additive manufacturing using infrared thermography. J Mater Process Technol. 2017;244:215-24. . ;:. Google Scholar
- Pham TQD, Hoang TV, Tran XV, Fetni S, Duchêne L, Tran HS et al. Characterization, propagation, and sensitivity analysis of uncertainties in the directed energy deposition process using a deep learning-based surrogate model. Probab Eng Mech. 2022;69:103297. . ;:. Google Scholar
- Pham TQD, Hoang TV, Tran XV, Fetni S, Duchêne L, Tran HS et al. A framework for the robust optimization under uncertainty in additive manufacturing. J Manuf Processes. 2023;103:53-63. . ;:. Google Scholar
- Wang Z, Jiang C, Liu P, Yang W, Zhao Y, Horstemeyer MF et al. Uncertainty quantification and reduction in metal additive manufacturing. npj Comp Mater. 2020;6(1):175. . ;:. Google Scholar
- Hamrani A, Agarwal A, Allouhi A, McDaniel D. Applying machine learning to wire arc additive manufacturing: A systematic data-driven literature review. J Intell Manuf. 2023:1-33. . ;:. Google Scholar
- Yaseer A, Chen H. Machine learning based layer roughness modeling in robotic additive manufacturing. J Manuf Processes. 2021;70:543-52. . ;:. Google Scholar
- Wang C, Tan XP, Tor SB, Lim CS. Machine learning in additive; 2020. . ;:. Google Scholar
- Qin J, Hu F, Liu Y, Witherell P, Wang CCL, Rosen DW et al. Research and application of machine learning for additive manufacturing. Addit Manuf. 2022;52:102691. . ;:. Google Scholar
- Meng L, McWilliams B, Jarosinski W, Park HY, Jung YG, Lee J et al. Machine learning in additive manufacturing: a review. JOM. 2020;72(6):2363-77. . ;:. Google Scholar
- Mozaffar M, Paul A, Al-Bahrani R, Wolff S, Choudhary A, Agrawal A et al. Data-driven prediction of the high-dimensional thermal history in directed energy deposition processes via recurrent neural networks. Manuf Lett. 2018;18:35-9. . ;:. Google Scholar
- Pham TQD, Hoang TV, Van Tran X, Pham QT, Fetni S, Duchêne L et al. Fast and accurate prediction of temperature evolutions in additive manufacturing process using deep learning. J Intell Manuf. 2023;34(4):1701-19. . ;:. Google Scholar
- Roy M, Wodo O. Data-driven modeling of thermal history in additive manufacturing. Addit Manuf. 2020;32:101017. . ;:. Google Scholar
- Cunningham CR, Wikshåland S, Xu F, Kemakolam N, Shokrani A, Dhokia V et al. Cost modeling and sensitivity analysis of wire and arc additive manufacturing. Procedia Manuf. 2017;11:650-7. . ;:. Google Scholar
- Pinto JM, Arrieta C, Andia ME, Uribe S, Ramos-Grez J, Vargas A et al. Sensitivity analysis of geometric errors in additive manufacturing medical models. Med Eng Phys. 2015;37(3):328-34. . ;:. PubMed Google Scholar
- Wang C, Tan XP, Tor SB, Lim CS. Machine learning in additive manufacturing; 2020. . ;:. Google Scholar
- Smith-Renner A, Fan R, Birchfield M, Wu T, Boyd-Graber J, Weld DS et al. No explainability without accountability: an empirical study of explanations and feedback in interactive ml. In: Proceedings of the 2020 chi conference on human factors in computing systems; 2020, April. p. 1-13. . ;:. Google Scholar
- Sarhan M, Layeghy S, Portmann M. Evaluating standard feature sets toward increased generalisability and explainability of ML-based network intrusion detection. Big Data Res. 2022;30:100359. . ;:. Google Scholar
- Lundberg SM, Su-In Lee. A unified approach to interpreting model predictions. Adv Neural Inf Process Syst. 2017;30. . ;:. Google Scholar
- Preece A. Asking'Why'in AI: explainability of intelligent systems-perspectives and challenges. Intell Syst Acc Fin Manag. 2018;25(2):63-72. . ;:. Google Scholar
- Lustig C, Rosner D. From explainability to ineffability? ML tarot and the possibility of inspiriting design. In: Designing Interactive Systems Conference; 2022, June. p. 123-36. . ;:. Google Scholar
- Lee SH. CMT-based wire arc additive manufacturing using 316 L stainless steel: effect of heat accumulation on the multi-layer deposits. Metals. February 2020;10(2):Art no. 2. . ;:. Google Scholar
- Goldak J, Chakravarti A, Bibby M. A new finite element model for welding heat sources. Metall Trans B. June 1984;15(2):299-305. . ;:. Google Scholar
- Lundberg SM, Erion G, Chen H, DeGrave A, Prutkin JM, Nair B et al. From local explanations to global understanding with explainable AI for trees. Nat Mach Intell. 2020;2(1):56-67. . ;:. PubMed Google Scholar
- Mitchell R, Frank E, Holmes G. GPUTreeShap: massively parallel exact calculation of SHAP scores for tree ensembles. PeerJ Comput Sci. 2022;8:e880. . ;:. PubMed Google Scholar
- Winter E 2002. The shapely value. Handbook of game theory with economic applications, 3, 2025-54. . ;:. Google Scholar
- Akossou AYJ, Palm R. Impact of data structure on the estimators R-square and adjusted R-square in linear regression. Int J Math Comput. 2013;20(3):84-93. . ;:. Google Scholar
- Vidyullatha P, Rao DR. Machine learning techniques on multidimensional curve fitting data based on R-square and chi-square methods. Int J Electr Comput Eng. 2016;6(3):974. . ;:. Google Scholar
