Design and modeling of the nonlinear properties of octagonal lattice Ge20Sb5Se75 photonic crystal fibers

Abstract

Most silica photonic crystal fibers have limited spectral broadening in the infrared region, making them less than ideal in terms of technological applications. In this work, we propose a new Ge20Sb5Se75 chalcogenide octagonal photonic crystal fiber that provides diverse dispersions with all-normal and anomalous regimes and multiple zero-dispersion wavelengths. The nonlinear properties are investigated over a wide wavelength range up to 14 µm by numerically solving Maxwell's wave equations using Lumerical Mode Solutions software. The full-vector finite-difference eigenmode method minimizes the losses so that low confinement losses in the short-wavelength region of 1 − 6 µm are found and nonlinear coefficients as high as thousands of W−1.km−1 are achieved. Three fibers with an all-normal dispersion profile and anomalous dispersion with one or three zero dispersion wavelengths are proposed for supercontinuum generation. The fibers provide small dispersion values of −0.88, 0.08, and 1.646 ps/(nm.km) at suitable pump wavelengths. Furthermore, the very small confinement loss of approximately 10−5 to 10−11 dB/m is the outstanding advantage of these optical fibers. A broadband spectrum with low input power is expected as a result of the proposed fiber-based supercontinuum generation.

INTRODUCTION

Broadening the output pulse in the mid-infrared (MIR) and infrared (IR) spectral regions is difficult when silica photonic crystal fibers (PCFs) are used for supercontinuum (SC) generation due to the high material absorption of glass. This is also the main limitation of silica PCFs, although this material is very popular and very easy to spin. To overcome this problem, many solutions, such as silica PCFs with various geometries 1 , 2 or liquid infiltration into hollow cores 3 , 4 , have been demonstrated to further improve their SC generation performance. However, the application of these PCFs in wide wavelength ranges (MIR, IR) is still a major challenge for research groups. In recent years, chalcogenide (ChG) glasses have become known as excellent nonlinear materials with the ability to provide SC spectra in a wavelength range as wide as 20 μm 5 , 6 . Compared with silica, ChG glasses have higher optical transparency, higher linear and nonlinear refractive indices, lower phonon energy and greater optical transparency 7 . These compounds are formed mainly by chalcogenized elements of group XVI (S, Se and Te) and covalently bonded to Ge, As and Sb of group XV or Ge and Si of group XIV. Along with the flexibility in the structural design of PCFs, these beneficial properties are exploited and demonstrated numerically or experimentally for generating very broad bandwidths and highly coherent SC sources.

By numerical simulation, work 8 reported that As ₂ Se ₃ hexagonal PCFs can produce low dispersion values of 19.92, 8.19, 4.06, and 15 ps. (nm/km) at pump wavelengths of 2.05, 3.1, 3.5, and 4.0 µm, respectively, with variations in the lattice constant Ʌ and the filling factor d / Ʌ ( Ʌ = 1.0 µm, d / Ʌ = 0.8; Ʌ = 2.5 µm, d / Ʌ = 0.6; Ʌ = 3.0 µm, d / Ʌ = 0.5; and Ʌ = 3.5 µm, d / Ʌ = 0.5). These PCFs enabled SC with a spectrum extension from 2 to 15 µm. Article 9 numerically proved that a Ge ₁₅ Sb ₁₅ Se ₇₀ circular lattice-PCF has an all-normal dispersion profile with a small effective mode area and high Kerr nonlinearity up to 1.96 W ⁻¹ .m ⁻¹ at 3 μm, but the investigated wavelength area is only up to 8 μm. The effective mode area and nonlinear coefficient of Ga ₈ Sb ₃₂ S ₆₀ -PCF ( Ʌ = 2.5 µm, d / Ʌ = 0.352) with a hexagonal structure of 10 are 15.23 µm ² and 970 W ⁻¹ .km ⁻¹ at 4.5 µm, respectively, as verified by simulations of ultraflat MIR SC generation. A Ga ₈ Sb ₃₂ S ₆₀ -PCF with a length of 9 mm and rectangular core was demonstrated to generate SC spectra with a MIR broadband due to its small all-normal dispersion. The values change from −19.52 ps/(nm.km) to −11.78 ps/(nm.km) at a pump wavelength of 4.0 µm as diameter d ₁ increases from 1.3 to 1.9 µm with Λ = 2.5 µm 11 . Adjusting the diameter d of the air holes in the hexagonal cladding of As ₃₉ Se ₆₁ -PCF dominated the dispersion properties in favor of SC generation in the MIR region. Additionally, a PCF with Λ = 2.5 µm and d = 0.7 µm was reported to have a small effective mode area and a high nonlinear coefficient at 3.45 µm, which are 6.8 µm ² and 5.89 W ⁻¹ .m ⁻¹ , respectively 12 . The generation of SCs in the MIR region with high coherence was reported in 13 based on GeSe ₂ -As ₂ Se ₃ -PbSe-PCFs with optimized dispersion. A dispersion value of −100 ps/(nm.km) at 3.1 µm was found for the structure Λ = 2.5 µm, d = 1.3 µm, but the nonlinearity was not as high as approximately 100 W ⁻¹ km ⁻¹ with d = 0.65. Reference 14 also numerically analyzed the possibility of enabling MIR ultrabroadband SC generation based on a Ge _11.5 As ₂₄ Se _64.5 -circular PCF with a low dispersion value. The variation in the lattice constant Λ ₁ leads to a variation in the dispersion, the value of which varies from −2.62 ps/(nm.km) at Λ ₁ = 1.68 μm to −0.69 ps/(nm.km) at Λ ₁ = 1.75 μm. Furthermore, the effective mode area also changes from 5.66 μm ² to 5.30 μm ² when Λ ₁ is adjusted from 1.75 to 1.70 μm.

In the present study, ChG-PCFs were fabricated quite conveniently using stack-and-draw methods, and the mid-infrared SC generation spans ∼2.0 to 15.1 μm in 3 cm long As ₂ Se ₃ and AsSe ₂ fibers. Additionally, Ge ₁₅ Sb ₂₀ Se ₆₅ -PCFs spun into bare glass fibers have a loss of approximately 1.68 dB/m at 6.0 μm according to the melt-quenching method; these fibers are good candidates for highly sensitive temperature sensors 15 , 16 . Different methods, such as the casting method 17 , combined extrusion method 18 , and rod-in-tube drawing technique 19 , have been shown to improve and enhance the quality of ChG-based SC generation-PCFs.

Obviously, ChG-PCF, as an interesting nonlinear medium for SC generation in the IR and MIR regions, has been verified through previous publications. The variations in the geometry of the lattice, the arrangement of the air holes in the cladding, and even the variety in the shape design of the core strongly influence the improvement in the dispersion and nonlinear properties of the fibers. Lattice types with high symmetry, such as hexagonal, circular, rectangular, and suspended cores, are preferred for design, but changing many lattice parameters at the same time can lead to complex fiber manufacturing. There are very few papers mentioning octagonal ChG-PCFs, and publication 20 showed the ability to improve the dispersion of octagonal As ₂ Se ₃ -PCFs. The values of characteristic quantities such as dispersion, nonlinear coefficient, and effective mode area are 77.55 ps/(nm.km), 4506 W ⁻¹ .km ⁻¹ , and 6 µm ² , respectively, at 1.55 µm, which is suitable for SC generation.

The dispersion properties and nonlinear properties of Ge ₂₀ Sb ₅ Se ₇₅ -PCFs over a broad wavelength range up to 14 µm are investigated in numerical detail and reported in this work. The same air holes are arranged evenly in the cladding in an octagonal fashion. A flat dispersion with a very small value of approximately 1.0 ps/(nm.km) and high nonlinearity coefficients of thousands of W ⁻¹ .km ⁻¹ are achieved. Interestingly, very low confinement losses, as low as approximately 10 ⁻¹¹ dB/m at a suitable pump wavelength, were obtained. This makes the proposed optimal PCFs quite necessary for broadband SC generation in the MIR region with low peak power.

MATERIALS-METHODS

Lumerical Mode Solutions software assisted us in designing the structures of the Ge ₂₀ Sb ₅ Se ₇₅ -PCFs. First, the Ge ₂₀ Sb ₅ Se ₇₅ material is introduced into the data system by determining the Sellmeier coefficient of the linear refractive index according to Equation ( 1 ) 21 . Second, we build a subroutine for the octagonal structure. There are eight layers of air holes with diameter d = (0.3 − 0.75) Ʌ , with Ʌ being the distance between two adjacent holes (lattice constant) surrounding a core with diameter D c = 2 Ʌ − d . The values of Ʌ are 2.2, 2.5, 4.5, and 5.0 µm. The position of the air holes is calculated so that they are evenly spaced and parallel to the axis of the core and then attached to the system. Finally, we chose the refractive indices of the air in the available data to determine the entrance into the holes in the cladding. The shape of the PCF in two dimensions is illustrated in Figure 1 a. The refractive index of the Ge ₂₀ Sb ₅ Se ₇₅ material was extrapolated according to 21 and is shown in Figure 1 b. The values decrease with increasing wavelength, but the decrease in the refractive index is faster in the short-wavelength region from 1 to 2 µm.

where λ is the wavelength and n ( λ ) is the refractive index of the material.

Figure 1 . The shape of Ge ₂₀ Sb ₅ Se ₇₅ -PCF in two-dimensional space with the core in the center and eight surrounding layers of air holes. The white represents air filling into the holes and the green represents the Ge ₂₀ Sb ₅ Se ₇₅ base material ( a ). The decrease of linear refractive index with respect to wavelength is extrapolated according to ²¹ ( b ).

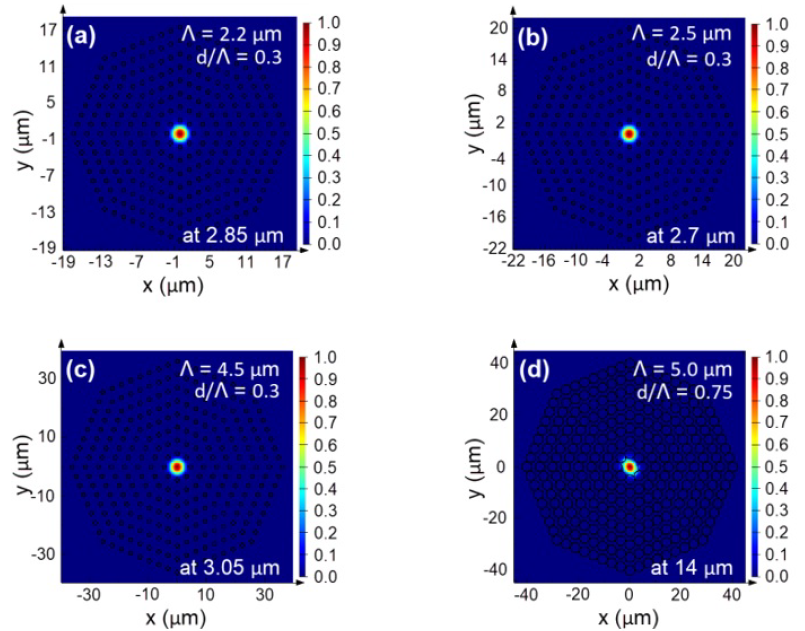
The propagation of electromagnetic modes in nonlinear media such as Ge ₂₀ Sb ₅ Se ₇₅ -PCFs is modeled by solving Maxwell's wave equations. The cross-section of the fibers is divided into a very large number of very small rectangles to minimize losses using the full-vector finite-difference eigenmode method. Furthermore, the boundary condition is chosen to be perfectly matched layers to help maximize light absorption and minimize reflection at the boundary. The good light confinement in the core of Ge ₂₀ Sb ₅ Se ₇₅ -PCFs is illustrated in Figure 2 .

Dispersion is a typical phenomenon of optical fibers and is characterized by how fast the pulse's different frequency components move due to interactions with the electrons of the medium, described by Equation ( 2 ) 22 . PCFs with suitable dispersion properties, such as flatness over a wide wavelength range, small gradients, and low values at pump wavelengths, are always important factors in improving the quality of the SC process.

where Re[ n _eff ], λ , and c are the real parts of the effective refractive index, the wavelength, and the speed of light in a vacuum, respectively.

When the laser pulse propagates in an optical fiber, the quantity responsible for the dispersive temporal broadening of pulses is expressed in the group velocity dispersion (GVD) parameter ( β ₂ ) as follows 20 :

Further SC spectral broadening at the edges depends on the nonlinear characteristics of PCFs, such as confinement loss ( L _c ), the nonlinear coefficient ( γ ), and the effective mode area ( A _eff ), which are determined through the following formula 22 :

where Im [ n _eff ] is the imaginary part of the effective refractive index. The confinement loss is one of the characteristic quantities of PCFs; it represents the degree to which information is confined in the core and is not scattered when the laser pulse is transmitted. Structural parameters such as the air hole diameter and lattice constant affect the confinement loss.

where n ₂ is the nonlinear refractive index of Ge ₂₀ Sb ₅ Se ₇₅ . The nonlinear coefficient quantifies the strength of the nonlinear interaction relative to the Kerr nonlinearity of the medium. PCFs with higher nonlinearities are more beneficial for low-peak power SC sources. The nonlinear coefficient quantifies the strength of the nonlinear interaction relative to the Kerr nonlinearity of the medium. PCFs with higher nonlinearities are more beneficial for low-peak power SC sources. The nonlinear coefficient is inversely proportional to the effective mode area, which represents the area that the wave guide or fiber mode effectively covers in terms of transverse dimensions.

Figure 2 . The images illustrate the confinement of light in the core of Ge ₂₀ Sb ₅ Se ₇₅ -PCFs.

RESULTS

Normal and anomalous dispersion is achieved in optical fibers due to the increase or decrease in the refractive index with increasing wavelength. Typically, a normal dispersion is observed as the refractive index decreases with increasing wavelength. However, in small wavelength ranges, the absorption of radiation causes the refractive index to increase with increasing wavelength, a phenomenon known as anomalous dispersion.

Ge ₂₀ Sb ₅ Se ₇₅ -PCFs have diverse dispersion properties over a wide wavelength range, as shown in Figure 3 . Most anomalous dispersions with one, two or even three zero dispersion wavelengths (ZDWs) are found. There is only one all-normal dispersion for a PCF with structure Λ = 2.2 µm and d / Λ = 0.3. For small PCFs ( Λ = 2.2 and 2.5 µm), the majority of the dispersion curves have a typical parabolic profile, separating normal and anomalous dispersion regions in the investigated wavelength range. When Λ = 2.2 µm, except for the only all-normal dispersion curve, the remaining structures all have anomalous dispersion with two ZDWs in the wavelength range up to 8 µm. For PCFs with Λ = 2.5 µm, we obtain two dispersion curves with three ZDWs corresponding to the structures Λ = 2.5 µm, d / Λ = 0.3 and Λ = 2.5 µm, d / Λ = 0.35. When the size of the PCFs is further increased ( Λ = 4.5 and 5.0 µm), only anomalous dispersion curves are observed with one ZDW. Furthermore, the dispersion curves tend to shift above the zero dispersion curve as d / Λ increases from 0.3 to 0.75. Therefore, ZDW _1s increasingly shift toward shorter wavelengths, while ZDW _2s and ZDW _3s shift toward longer wavelengths.

Figure 3 . The all-normal and anomalous dispersions with multiple ZDWs of Ge ₂₀ Sb ₅ Se ₇₅ -PCFs when d / Λ varies from 0.3 to 0.75, with Λ = 2.2 µm ( a ), 2.5 µm ( b ), 4.0 µm ( c ), and 5.0 µm ( d ).

Table 1 shows the values of ZDWs when Λ and d / Λ vary. The ZDW ₁ of PCFs with Λ = 2.2 and 2.5 µm has a value close to the wavelength of 1.55 µm, which is the wavelength of common commercial laser sources. This finding implies that we choose appropriate pump wavelengths for SC generation. However, some studies on ChG-PCFs 5 , 8 , 9 have verified that suitable pump wavelengths can be selected in the MIR or IR region. Due to the rapid development of fiber optic technology today, choosing a pump wavelength in any region is feasible in practice.

Table 1 The ZDWs of Ge ₂₀ Sb ₅ Se ₇₅ -PCFs with variations in Λ and d / Λ

Figure 4 . The graph of GVD against wavelength of Ge ₂₀ Sb ₅ Se ₇₅ -PCFs when d/Λ vary from 0.3 to 0.75, with Λ = 2.2 µm ( a ), 2.5 µm ( b ), 4.5 µm ( c ), and 5.0 µm ( d ).

The relationships between the GVD parameter and wavelength and between the GVD parameter and the variation in the structural parameters are shown in Figure 4 . In the wavelength region smaller than approximately 4 µm, the difference in GVD values of the structures is not large. At best, the separation between the curves is clearer in the longer wavelength region. The GVD will be either positive or negative depending on whether the fiber is a normal or anomalous dispersive type. The GVD increases rapidly in the wavelength region greater than 6 µm.

Based on the preliminary dispersion and GVD parameter results, three optical fibers with suitable dispersion and GVD values are introduced to study in detail the characteristic quantities required for the SC process. The names of the fibers are #F ₁ , #F ₂ , and #F ₃ , with the structural parameters Λ = 2.2 µm, d / Λ = 0.3; Λ = 4.5 µm, d / Λ = 0.3; and Λ = 2.5 µm, d / Λ = 0.3. Figure 5 − Figure 9 displays the dispersion and quantities that characterize the nonlinear properties of the three fibers. The values of dispersion, GVD parameter, confinement loss, nonlinearity coefficient, and effective mode area at the pump wavelengths are calculated and indicated in Table 2 .

Figure 5 . The dispersions curves with multiple ZDWs of proposed fibers, #F ₁ ( Λ = 2.2 µm, d / Λ = 0.3), #F ₂ ( Λ = 4.5 µm, d / Λ = 0.3), and #F ₃ ( Λ = 2.5 µm, d / Λ = 0.3) ( a ). The dispersion values of fibers at pump wavelengths ( b ).

Figure 6 . The dependence of GVD parameter on the wavelength of proposed fibers, #F ₁ ( Λ = 2.2 µm, d / Λ = 0.3), #F ₂ ( Λ = 4.5 µm, d / Λ = 0.3), and #F ₃ ( Λ = 2.5 µm, d / Λ = 0.3) ( a ). The GVD parameter values of fibers at pump wavelengths ( b ).

Figure 7 . The dependence of confinement loss on the wavelength of proposed fibers, #F ₁ ( Λ = 2.2 µm, d / Λ = 0.3), #F ₂ ( Λ = 4.5 µm, d / Λ = 0.3), and #F ₃ ( Λ = 2.5 µm, d / Λ = 0.3) ( a ). The confinement loss values of fibers at pump wavelengths ( b ).

Figure 8 . The dependence of nonlinear coefficient on the wavelength of proposed fibers, #F ₁ ( Λ = 2.2 µm, d / Λ = 0.3), #F ₂ ( Λ = 4.5 µm, d / Λ = 0.3), and #F ₃ ( Λ = 2.5 µm, d / Λ = 0.3) ( a ). The nonlinear coefficient values of fibers at pump wavelengths ( b ).

Figure 9 . The effective mode area on the wavelength of proposed fibers, #F ₁ ( Λ = 2.2 µm, d / Λ = 0.3), #F ₂ ( Λ = 4.5 µm, d / Λ = 0.3), and #F ₃ ( Λ = 2.5 µm, d / Λ = 0.3) ( a ). The effective mode area values of fibers at pump wavelengths ( b ).

Table 2 The structural parameters and the values of the characteristic quantities at the pump wavelength of the three proposed fibers

DISCUSSION

Dispersion is a very important factor in choosing a suitable fiber for SC processes with all-normal or anomalous dispersion characteristics. In addition, the number of ZWWs in dispersion profiles governs the spectral characteristics related to soliton dynamics. Fiber #F ₁ ( Λ = 2.2 µm, d / Λ = 0.3) possesses all-normal dispersion and has a local maximum at a wavelength of approximately 2.8 µm ( Figure 5 ). The expected pump wavelength for SC generation is 2.85 µm. A low dispersion value of −0.88 ps/(nm.km) was obtained at this wavelength ( Table 2 ). Compared to previous publications on SCs based on ChG-PCFs with all-normal dispersion, the dispersion value achieved is approximately 13 times lower than 11 , 113 times lower than 13 , and 3 times lower than 14 . A low dispersion at a suitable pump wavelength is an ideal condition for enabling an SC with a boad spectrum and high coherence under the control of the self-phase modulation effect and optical wave breaking. This phenomenon occurs because the energy is transferred sequentially from high frequency to low frequency in the pulse by stimulated Raman scattering 23 , leading to the suppression of soliton dynamics. The dispersion curve of fiber #F ₂ ( Λ = 4.5 µm, d / Λ = 0.3) is divided into two regimes: normal and anomalous dispersion ( Figure 5 ), with ZDW = 3.048 µm. The recommended pump wavelength is 3.05 µm so that the fiber is pumped in an anomalous dispersion regime. Typically, the SC spectrum is much broader than that of a fiber pumped in the normal dispersion regime due to the impact of soliton effects such as soliton fission, self-shifting soliton frequency, and dispersion waves 24 , 23 , 25 . Moreover, with a very low dispersion value of 0.08 ps/(nm.km) at the pump wavelength ( Table 2 ), this fiber is expected to generate a high-quality SC. Fiber #F ₃ ( Λ = 2.5 µm, d / Λ = 0.3) has anomalous dispersion with three ZDWs, so the dispersion region is divided into four parts ( Figure 5 ). With a dispersion value of 1.646 ps/(nm.km) at 2.7 µm, close to ZDW ₁ (2.663 µm), the proposed fiber pumps are in the first anomalous dispersion regime, so soliton dynamics remain the main mechanism for broadening the SC spectrum. Furthermore, a soliton shift can occur from the first anomalous dispersion region to the second anomalous dispersion region, causing the spectrum to continue to broaden 26 . In addition, effects such as phase modulation and four-wave mixing are created on the left side of the ZDWs, causing a green shift in the trapped wave, which also helps increase the bandwidth 26 . The dispersion values obtained at the pump wavelength for fibers #F ₁ and #F ₂ are much lower than those in reference 8 . The GVD parameter is proportional to dispersion and characterizes the influence of the medium on the duration of an optical pulse. The GVD values at the pump wavelengths of the three proposed fibers are 3.756, −3.967, and −6.650 ps ² /m. Fiber #F ₁ has the lowest dispersion value corresponding to the smallest GVD.

The confinement loss of fibers #F ₁ , #F ₂ , and #F ₃ increases rapidly in the long-wavelength region ( λ > 5.0 µm) ( Figure 7 ) due to the leakage of low-frequency components from the core to the cladding or between air holes. This also leads to a large effective mode area in this wavelength region. In addition, the nonlinear coefficient is also reduced because it is inversely proportional to the effective mode area. Therefore, all the fibers had a pump wavelength chosen to be less than 5.0 µm. Among the three fibers, fiber #F ₂ has the smallest L _c value (1.549×10 ⁻¹¹ dB/m) and the lowest dispersion value compared to the others, but it has the largest effective mode area and smallest nonlinear coefficient ( Table 2 ). This opens up the opportunity to create broadband SCs using #F ₂ fibers. The larger the L _c is, the more the spectrum is limited to broadening at the red edge. It should be noted that it is difficult to simultaneously optimize the nonlinear characteristics of the fibers because the fibers are advantageous because they can be used to generate appropriate SC orientations. Fiber #F ₁ has the smallest effective mode area, leading to the highest nonlinear coefficient, and the dispersion value of −0.88 ps/(nm.km) is smaller than that of fiber #F ₃ . Although the L _c of this fiber is the largest among the three fibers, it is still quite small compared to that in some previous publications 5 , 8 . This fiber can be used as a broad-spectrum and low-peak-power SC source due to the high nonlinearity at the pump wavelength. Fiber #F ₃ is still expected to produce a broadband SC under the influence of soliton dynamics, although this approach does not have outstanding advantages when considering the value of nonlinear characteristic quantities. A rather small L _c value of 1.440×10 ⁻⁷ dB/m and a rather high nonlinearity coefficient of 921.717 W ⁻¹ .km ⁻¹ at a pump wavelength of 2.7 µm are necessary conditions for obtaining a broad-spectrum SC with low peak power. Moreover, soliton migration through different dispersion regions due to the existence of three ZDWs helps the SC spectrum continue to expand further.

The combination of two factors, the highly nonlinear Ge ₂₀ Sb ₅ Se ₇₅ substrate and the octagonal lattice of the designed structure, helped fibers #F ₁ , #F ₂ , and #F ₃ demonstrate outstanding advantages in terms of dispersion and nonlinear properties in the wavelength range up to 14 µm. These materials have a flat dispersion profile, low value and very small confinement loss suitable for broadband SC generation applications. Table 3 compares the dispersion values and characteristic quantities of the proposed PCF with those of other publications on the use of Ge-Sb-Se compounds.

Table 3 Comparison of characteristic quantities with those of other PCF publications using Ge-Sb-Se compounds

CONCLUSIONS

We designed and modeled forty Ge ₂₀ Sb ₅ Se ₇₅ -PCF structures with octagonal lattices. The dispersion and nonlinear properties of the fibers are investigated in detail over a wavelength range of up to 14 µm by numerically solving Maxwell's wave equations using the full-vector finite-difference eigenmode method. Based on the dispersion property and GVD parameter results, we propose three fibers with suitable characteristic quantities for determining the direction of SC generation. Fibers #F ₁ , #F ₂ , and #F ₃ have very low dispersions—−0.88, 0.08, and 1.646 ps/(nm.km)—at pump wavelengths of 2.85, 3.05, and 2.7 µm, respectively; these values are much lower than those of our previous publication 27 on Ge ₂₀ Sb ₅ Se ₇₅ -PCF with a hexagonal crystal lattice. In addition, the diversity in the dispersion profiles of the three fibers (all-normal dispersion and anomalous dispersion with one or three ZDWs) strongly influences the characteristics of the SC spectrum. With high nonlinear coefficients of 1010.043, 289.265, and 921.717 W ⁻¹ .km ⁻¹ and low confinement losses of 1.305×10 ⁻⁵ , 1.549×10 ⁻¹¹ , and 1.440×10 ⁻⁷ dB/m, respectively, three fibers are expected to create SCs with the spectrum broadened further toward the edges. Compared with previous publications, fiber #F ₁ has a nonlinear coefficient approximately 1.05 times greater than 10 , 2 to 3.5 times greater than 27 and approximately 10 times greater than that of publication 13 . The F3 fiber also has a nonlinear coefficient approximately 4 times greater than 27 . Moreover, the effective mode area is approximately 1.6 times smaller than 10 . Although the nonlinear coefficients of fibers #F ₂ and #F ₃ are lower than those of fibers 10 , 9 and 12 , they have a much lower confinement loss. These fibers with both all-normal and anomalous dispersion properties are suitable for broadband SC generation in the mid-infrared or infrared region to cover the molecular fingerprint spectral region where distinctive vibrational absorption features are exploited to identify the different molecules. The results of SC based on the #F ₁ fiber with a normal dispersion configuration can yield a wide spectrum, high coherence, and low noise. This approach is suitable for applications in the fields of optical coherence tomography and remote sensing 28 .

ABBREVIATIONS

SC : Supercontinuum

MIR : Mid-infrared

IR : Infrared

PCFs : Photonic Crystal Fibers

ChG : Chalcogenide

ZDW : Zero dispersion wavelength

GVD: Group Velocity Dispersion

COMPETING INTERESTS

The authors declare that they have no conflicts of interest.

AUTHORS’ CONTRIBUTIONS

Nguyen Thi Thuy: Methodology, designing and simulating the PCF structures, data processing, plotting the graph, writing the manuscript, answering the reviewer's questions, and providing supervision.

ACKNOWLEDGEMENTS

None