Nonlinear coupled constitutive relation model for monatomic gas in the OpenFOAM framework

Abstract

In high-speed rarefied gas flow simulations, the linear constitutive relations of the classical Navier-Stokes-Fourier (NSF) equations are no longer successfully applied. In the present work, the two-dimensional nonlinear coupled constitutive relations (NCCR) model of the monatomic gas in an algebraic-type form is successfully implemented in the rhoCentralFoam in OpenFOAM to simulate the high-speed rarefied gas flows. Methods: This solver initially resolves the NSF equations using high-resolution central schemes in the finite volume method. The implicit NCCR model is solved by the iterative process with the initial values from the linear constitutive relations of the NSF model. After the convergence, these nonlinear constitutive relations are embedded in the NSF equations to continue the solution. Results: This new modified solver would be validated for the argon gas flows past a circular cylinder in cross-flow at Mach of 5 and Kn = 0.05 and the sharp leading edge flat plate at Mach of 4 and Kn = 0.0042. Conclusion: The simulation results show that the NCCR model agrees well with the DSMC data for the temperature contours for both cases and the temperature and velocity along the shock stand-off distance and is better than the NSF model in the high-speed rarefied gas simulations for the circular cylinder case.

INTRODUCTION

A precise numerical simulation of high-speed rarefied gas flows that solves the Navier‒Stokes Fourier (NSF) equations is needed to simulate computational fluid dynamics (CFD). In high-speed rarefied gas flows, thermal nonequilibrium may result from the high velocity and low gas density of the gas flow, represented by the Mach, Ma , and Knudsen, Kn , numbers. In viscous gas flows, the transfer of momentum is conducted by a velocity gradient, while the temperature gradient causes the transfer of heat energy. These transfers are presented as the effects of viscous stress and heat transfer. In the past, the NSF equations were proven to be limited by their ability to capture the correct flow physics of rarefied gas flows because they were derived from the continuum hypothesis. The viscous terms (shear stress and heat flux) are linearly proportional to the velocity and temperature gradients in the NSF equations. Due to the lack of molecular interactions, these methods have no longer been applied to rarefied gas flows because the continuum hypothesis is violated. Considerable research has been conducted to correct this problem for the NSF equations in the literature. An alternative approach to overcome these classical constitutive relations is the nonlinear coupled constitutive relation (NCCR) model in an algebraic-type form for monatomic gas, which was proposed in 1 , 2 based on Eu’s generalized hydrodynamic equations 3 . Then, the constitutive relationships, such as the stresses and heat fluxes, are generally nonlinear. These equations have been successfully applied for simulating rarefied gas flows where the NSF equations were not used.

This paper will first present the implementation of the NCCR model mentioned above for monatomic gases (such as argon) in the open-source software OpenFOAM by modifying the solver rhoCentralFoam . This solver initially solves the NSF equations using finite volume discretization and a high-resolution central scheme to simulate high-speed viscous gas flows. A subroutine of the iterative solution of the algebraic-type NCCR model in 1 , 2 is then embedded in this solver. In particular, a case in which an argon gas cross-flow passed through a circular cylinder 4 at a Mach number of Ma = 5 and Kn = 0.05 and a case in which a sharp leading edge flat plate was used at Ma = 4 and Kn = 0.0042 5 were adopted for investigating and validating this new modified solver. The Knudsen number, Kn , is computed by the ratio of the gas molecular mean free path before the collision, λ _∞ , to the characteristic length (i.e., the diameter of the circular cylinder or the length of the flat plate). This result also indicates the level of nonequilibrium in the rarefied gas flows. The hard-sphere (HS) model of monatomic gas is selected for testing two cases in the present study. The computational results in the present study will be compared with the DSMC data. The direct simulation Monte Carlo (DSMC) method successfully simulates high-speed rarefied gas flows for all Knudsen numbers, but the computational effort is expensive. The DSMC method has yielded more precise computational results in high-speed rarefied gas flow simulations than did the use of continuum flow models such as the NSF equations 6 . Therefore, the DSMC method has been used to validate the CFD results solved by the NSF equations in the literature. With appropriate slip and jump boundary conditions, the NSF equations may successfully simulate high-speed rarefied gas flows in the continuum regime up to a Kn of 0.1. The computational cost of the NSF solution is much less than that of the DSMC method, especially for three-dimensional flows. The solver dsmcFoam in OpenFOAM is also chosen to generate the DSMC data of the considered cases to evaluate the accuracy of the NSF and NCCR calculated results.

NAVIER-STOKES-FOURIER GOVERNING EQUATIONS

The NSF equations were derived from conservation laws and were based on the continuum hypothesis. They that neglect body forces are described and presented in vector form as

Continuity equation

Momentum equation

where П is the viscous stress tensor and П = -2µ dev ( D ), where , and dev indicates the deviatoric stress of tensor ( D ) – (1/3)(tr)( D ) I , where tr is the trace. The equation p = ρRT computes the gas pressure .

Energy equation

where E = e + 0.5| u ² | and Q is the Fourier heat flux, Q = -k∇T. The NSF equations are numerically solved with the high-resolution central scheme in OpenFOAM 7 as the solver, namely, rhoCentralFoam .

NONEQUILIBRIUM SLIP AND JUMP BOUNDARY CONDITIONS

The slip and jump conditions must be applied to the surface to simulate high-speed rarefied gas flows. The Maxwell slip boundary condition was derived from conserving the tangential momentum at the surface. It includes the curvature effect and thermal creep and can be expressed in vector form as 8 :

where the tensor S = I - nn , where n is the normal outward vector, the normal velocity components are removed, and u _w is the surface velocity. The coefficient σ _u is the tangential momentum accommodation coefficient (0 ≤ σ _u ≤ 1). It denotes the proportion of molecules reflected diffusely and then equal to 1 − σ _u for specularly. The curvature effect term П _mc . The mean free path is calculated by

where the power law computes the viscosity µ for the hard sphere (HS) model,

where A _P = 0.970312 × 10 ^-6 ( Pa.s K ^0.5 ) for argon gas at the reference temperature of 273 K 9 .

According to the experimental observations, there is a difference between the gas temperature near the surface and the wall temperature, T _w . Therefore, the temperature jump condition was derived for computing rarefied gas simulations. The Smoluchowski temperature jump condition was first proposed by conserving the heat flux normal to the surface and is represented by 10 :

The coefficient σ _T is the thermal accommodation coefficient (0 ≤ σ _T ≤ 1). This parameter represents the energy exchange between the gas molecules and the surface. A value of 1 denotes perfect energy exchange, and no energy exchange corresponds to a value of 0.

IMPLICIT 2D NONLINEAR COUPLED CONSTITUTIVE RELATION (NCCR) MODEL FOR MONATOMIC GAS

The following 2D implicit NCCR model for conservation laws was developed based on Eu’s generalized hydrodynamic equations 3 . First, the heat fluxes and the stress components are normalized, and the symbol “^” represents the dimensionless quantity in the constitutive relations as follows:

In a 2D physical problem, the stresses ( П _xx , П _xy ) and heat flux ( Q _x ) are induced by thermodynamic forces that are represented by ( u _x , v _x , T _x ) and can be approximately solved by consisting of two parts: 1) ( u _x , 0, T _x ) and 2) (0, v _x , 0) 1 , 2 . Then, the equations of the first part are

where

The equations for the second part are

where

and the constraint

The values of the stresses and heat flux, П _xx , П _xy, and Q _x from the NSF governing equations are set as the initial values to solve the 2D NCCR model as follows iteratively:

The iterative solution was presented in detail in 1 , 2 . For the first part, to solve the quantities ( u _x , 0, T _x ):

If and are positive

If and are negative

and the subscript and terms and are computed by

For (0, v _x , 0), can be calculated from a given by 1 , 2

and can be calculated using the constraint above (equation (13)). This iterative loop converges within a few iterations with the converged criteria; then, the converged terms of the stresses and heat flux are implemented back into the numerical scheme, solving the NSF equations in the rhoCentralFoam as follows:

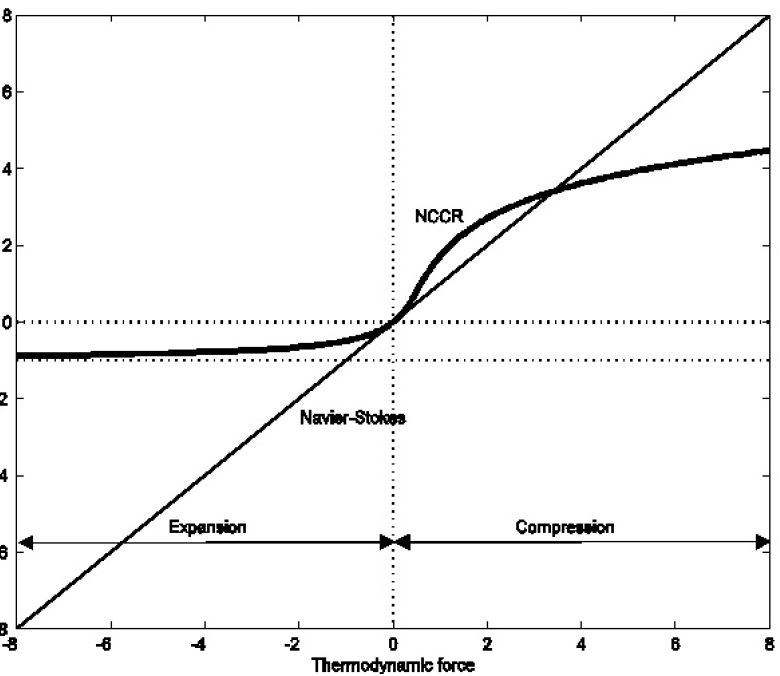
A typical nonlinear normal stress, , against the thermodynamic force (by velocity gradient ) of the NCCR and the linear NSF models in the expansion and compression flows is presented in Figure 1 1 . Figure 1 shows the asymmetry of the normal stress for the rapid compression and expansion of argon gas. The gas expands in the negative normal stress region and is compressed in the region of positive normal stress. The horizontal axis denotes the thermodynamic force represented by the velocity gradient, and the vertical axis represents the normal stress 2 . The nonlinearity of the normal stress is obvious in the NCCR model, while it is linear in the NSF model.

Figure 1 . Nonlinear and linear normal stresses, 1 .

The solver rhoCentralFoam will modify the diffusion terms in the momentum and energy equations to implement the 2D NCCR model. Moreover, the power law for calculating viscosity is also implemented in OpenFOAM. The 2D NCCR for a monatomic gas was first implemented in the solver rhoCentralFoam, OpenFOAM to simulate viscous gas flows.

NUMERICAL RESULTS

Circular cylinder in the cross-flow case

The high-speed argon gas cross-flow past a two-dimensional circular cylinder with a radius of R _C = 0.1524 m is shown in Figure 2 . The freestream conditions are the ones used in 4 except for the velocity, p _∞ = 0.234 Pa, T _∞ = 200 K _, u _∞ = 1312 m/s (Ma = 5), λ _∞ = 0.01524 m, T _{w =} 500 K, and Kn = 0.05 (the cylinder diameter as the characteristic length). The freestream conditions are maintained through the computational process. The condition zeroGradient is applied for the outlet boundary and the pressure at the surface. The condition symmetryPlane is set for the symmetry planes. The Maxwell and Smoluchowsi conditions are applied to the velocity and temperature at the surface, as shown in Figure 2 . The solver dsmcFoam in OpenFOAM was used for the DSMC simulation for the same considered case, using the HS model with a temperature exponent ω = 0.5, a reference temperature of 273 K, a molecular diameter of 4.17x10 ^- 10 m, and a mass of 66.3x10 ^- 27 kg. The structured mesh is designed to wrap the bow shock, and the final smallest size of the mesh is approximately λ _∞ /3 for both CFD and DSMC simulations 11 , 12 . The value of unity is adopted for the terms σ _u and σ _T in both the CFD and DSMC cases.

Figure 2 . Computational domain of the circular cylinder in cross-flow case.

A comparison of the temperature contours predicted by the NSF, NCCR, and DSMC models is shown in Figure 3 a and Figure 3 b, respectively. There are bow shocks with a fair shock stand-off distance from the cylinder surface. The high-temperature region also appears behind the shockwave. The thermal boundary layer is also shown near the cylinder surface. Overall, all the NSF, NCCR, and DSMC contours generally agree well. However, the NCCR model yields better results than does the NSF model for predicting the temperature contours in the core of the shock region.

Figure 3 . Temperature contours of the circular cylinder case a) NSF and DSMC models, and b) NCCR and DSMC models.

Figure 4 . Temperature distribution along the stand-off distance.

Figure 5 . Velcotiy magnitude distribution along the stand-off distance.

Figure 6 . Slip velocity distribution along the cylinder surface.

The calculated temperatures and velocity magnitudes along the shock stand-off distance are presented in Figure 4 and Figure 5 , respectively. All calculated temperatures are initially equal to the freestream values, and thereafter, they gradually increase in the bow shock region due to the compressed flow. Otherwise, the velocity magnitudes are initially at the freestream values before decreasing progressively in the core of the bow shock region. A comparison between the DSMC and CFD results showed that the NCCR model results are close to the DSMC data, while those obtained using the NSF model are not.

For completeness of the circular cylinder case, the slip velocity distributions of all the simulations are shown in Figure 6 , and they are plotted against the x -direction distance, as shown in Figure 2 . All slip velocities gradually increase in the 0 ≤ x ≤ 0. 23 m range, and the CFD and DSMC results differ. They reach the highest values around the location x = 0.25 m. The separation point is nearly the location x = 0. 25 m , and the gas flow reaches the wake region. Then, all the velocities gradually decrease to x = 0. 3048 m , and they are close together. Overall, the NCCR slip velocity is relatively close to that of the DSMC over the cylinder surface, with an average error of 21.84%, while the slip velocity is 22.67% for the NSF model.

Sharp leading-edge flat plate case

A schematic of the computational domain and the boundary conditions applied in the sharp leading edge flat plate case are shown in Figure 7 . The freestream argon flow conditions in the flat plate cases include p _∞ = 3.73 Pa, T _∞ = 64.5 K 5 , u _∞ = 631 m/s (Ma = 4), λ _∞ = 0.23 mm, T _{w =} 300 K, and Kn = 0.0042 (the length of the flat plate, l = 55 mm as the characteristic length). The boundary conditions, such as the zerGradient and symmetry planes, are applied for the other boundaries; see Figure 7 . The HS model of argon gas is still used for this case for CFD and DSMC simulations. The parameters needed for the DSMC simulations are similar to those of the circular cylinder case mentioned above. The structured mesh of the flat plate case is rectangular. It is quite simple and is not shown here. The final smallest size of the mesh is adopted from previous work 11 as follows: ∆x = ∆y = 0.35λ _∞ for the NSF and NCCR simulations and approximately λ _∞ /3 for the DSMC simulation. The Maxwell and Smoluchowski boundary conditions are applied for the surface in CFD simulations, and σ _u = σ _T = 1 in both CFD and DSMC runs. The DSMC data are also generated by the solver dsmcFoam to validate the CFD results.

Figure 7 . A numerical setup of the sharp leading edge flat plate case.

Figure 8 . Temperature contours of the flat plate cases a) NSF and DSMC models, and b) NCCR and DSMC models.

Figure 9 . Distribution of the slip velocity along the flat plate.

The NSF, NCCR, and DSMC temperature contours are plotted in Figure 8 a and 8b. The viscous effects at the sharp leading edge form curved shocks and develop the boundary layer. This layer is different from that used in the NSF and NCCR simulations with the DSMC simulation. Overall, there is relative agreement between the computational domain's CFD and DSMC temperature contours. As expected, there is little difference between the NSF and NCCR models for the sharp leading-edge flat plate case due to the small Knudsen number, Kn = 0.0024, for the flat plate case considered.

The slip velocity distributions along the flat plate are shown in Figure 9 and are plotted against the x -distance running along the surface. The slip velocities reach their peak values at the leading edge due to the high-nonequilibrium effect 12 . These velocities are 1) 370 m/s for the NSF simulation, 2) 354 m/s for the NCCR simulation, and 337 m/s for the DSMC data. The NCCR peak value is close to that of the DSMC. They gradually decrease along the flat plate past the sharp leading edge until reaching the trailing edge, and the DSMC slip velocity increases due to the separated flows, while those of the NSF and NCCR do not. The NSF and NCCR slip velocities relatively approach the DSMC data along the flat plate.

CONCLUSION

An implicit 2D NCCR model was successfully implemented in OpenFOAM by modifying the solver rhoCentralFoam . In addition, this modified solver was initially validated by investigating high-speed rarefied gas cross-flow past a circular cylinder and flow past a sharp leading-edge flat plate. The NCCR simulations run with the modified solver achieved stability. The simulation results of the NCCR model generally agreed better with the DSMC data than did those of the NSF model, especially for the circular cylinder case. This also proves that diffusion terms such as stresses and heat flux are more significant in obtaining CFD solution accuracy in high-speed rarefied gas flow simulations. Finally, an iterative loop is added to solve the nonlinear constitutive relations in the NCCR model, and the nonlinear constitutive relations reach a converged solution after a few iterations. Therefore, the computational time for a solution with the NCCR model is longer than 20% that of the NSF model. Further work will be conducted to implement and validate the 2D NCCR model for diatomic gases in the OpenFOAM framework with the solver rhoCentralFoam .

AUTHOR’S CONTRIBUTIONS

The authors have contributed equally to the present work in terms of the investigation, methodology, validation, visualization, review, and editing.

FUNDING

This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 107.03-2021.22.

COMPETING INTERESTS

The authors declare that they have no competing interests.

LIST OF SYMBOLS

CFD Computational Fluid Dynamics

DSMC Direct Simulation Monte Carlo.

NSF Navier–Stokes–Fourier.

NCCR nonlinear coupled constitutive relation.

E Total energy.

e Internal energy.

k Thermal conductivity.

Kn Knudsen number.

Ma Mach number.

p Pressure.

R Specific gas constant.

t Time.

T Temperature.

I Identity tensor.

Q Heat flux.

u Velocity.

Π Stress tensor.

ρ Gas density.

μ Viscosity.

γ Heat capacity ratio.

Pr Prandtl number.

Subscript

_W Wall.

∞ Freestream conditions.