Analysis of 12C+12C scattering using different nuclear density distributions

Abstract

Elastic ¹²C+¹²C angular distributions at three bombarding energies of 102.1, 112.0 and 126.1 MeV were analyzed in the framework of optical model (OM) and compared to the experimental data. The reality of the OM analysis using the double folding potential depends on the chosen nuclear density distributions. In this work, we use two available models of nuclear density distributions obtained from the electron scattering experiments and the density functional theory (DFT). The OM results show that the former gives better description of the ¹²C nuclear density distribution than the latter. Therefore, the DFT should be worked on for improving the nuclear density description of ¹²C in the future.

Introduction

One of the approaches which we have been utilizing to study nuclear properties is investigation of collisions of two particles, especially systems of two light heavy nuclei, such as ¹² C+ ¹² C 1 . Because of the refractive effect, the scattering data of this system gives information of nuclear potential in a wider range in comparison to what the heavy nuclei systems can give. In fact, when two heavy nuclei start overlapping each other, a strong absorption dominates at the surface, and leads to non-elastic processes. This phenomenon reduces the possibility of other effects which take place in the inner region of the nuclei and, thus, prevents us from getting any information about the nuclear potential in this region. Fortunately, the refractive effect, which happens in the inner region, can be observed in the data of large angles of elastic scattering of light heavy systems 2 , enabling these systems to become prominent objects to study either theoretically or experimentally.

One well-known model, which is able to handle the calculation of the scattering of two particles, is the optical model (OM). In this model, a complex potential, a so-called optical potential (OP), is utilized to describe both elastic scattering and non-elastic processes. There are two main approaches which have been used to obtain the OP. One is the phenomenological method in which parameters of the Woods-Saxon form are determined by experimental data. Another consists of microscopic models which are derived from nucleon-nucleon (NN) interactions. The latter approach is able to give a physical interpretation to experimental data because of its basic physical ingredients 2 ; therefore, microscopic models are an appealing topic to study.

One of such microscopic models is the double folding model in which the NN interactions and nuclear density of two particles are two crucial inputs. In recent years, D. T. Khoa et al . have developed an energy and density-dependent NN interaction, namely the effective CDM3Yn 3 . For the nuclear density, the Fermi form, which is obtained from electron scattering experiments 4 , is a classical distribution. Besides the studies of improving the density approximations for the folding potential, approaches which have been developed to study nuclear structure are also able to yield the nuclear density. Furthermore, the density functional theory (DFT) for nuclear studies was developed by P. Ring et al . 5 6 , the Green’s function Monte Carlo (GFMC) technique was investigated in the work of J. Carlson et al . 7 , and the ab initio calculation was studied by M. Gennari et al . 8 . It is important to study nuclear reaction by applying these methods to obtain the density of particles, before putting it into the double folding potential to calculate cross section.

The aim of this work was to compare the density distributions which are calculated in the framework of DFT and the Fermi form by OM analysis of elastic ¹² C+ ¹² C scattering data. In particular, these densities are put into the double folding potential to calculate angular cross sections of the ¹² C+ ¹² C system, before comparison with the experimental data.

Methods

Optical model

In the scenario of OM, the nucleus is assumed as a cloudy ball that absorbs and scatters partially the incoming particle flux in a similar way to the behavior of light. To describe this idea, the total potential (called the OP) is defined in term of a complex function,

where the second term accounts for the non-elastic scattering channels. Three parameters of W, R ₀ , and a correspond to the depth, radius and surface diffuseness parameters adjusted to obtain the best fit to the angular distribution data. V _C is the Coulomb potential. The real part of nuclear potential V _R (depicting the elastic channel) is calculated within the double folding model 2 3 9 using the effective NN interaction as follows:

where and correspond to the single-particle wave functions of the nucleon i in the target and the nucleon j in the projectile. With the explicit treatment of these single-particle wave functions of and , we can obtain the direct term and exchange term , given as 9 :

Here, v _D and v _EX are the direct and exchange terms of the effective NN interaction. is the relative distance between two interacting nucleons. Additionally, r _A and r _a are the nucleon coordinates with respect to target A and projectile a, respectively; R represents the nucleus-nucleus separation; and E and K correspond to the center of mass energy of the system and the relative momentum.

In the framework of quantum scattering theory, the differential cross section for an elastic scattering process is defined as 10 :

where the nuclear scattering amplitude is expressed in terms of partial-wave ,

and η is the Sommerfeld parameter and k is the wave number of the incident nucleus. The nuclear and Coulomb phase shifts ( i.e ., and ) are determined by the relative-motion wave function. Note, in the Schrödinger equation and the known U _OP (R) are shown below 10 :

Nuclear Density

To perform the OM calculations with the microscopic nuclear potential, the nuclear densities of colliding nuclei were required as the important inputs. In general, the nuclear density can be determined from the electron scattering experiment or DFT calculation.

The nuclear charge-density distribution or the nuclear root-mean-square (rms) charge radius is given by the form factor measurement in the electron scattering experiment 4 . Generally, the nuclear charge-density distributions are parameterized in terms of the two-parameter Fermi functions as follows:

where the parameters ( ) are chosen to reproduce correctly the nuclear rms charge radii.

On the other hand, nuclear density distributions can also be calculated by the framework of relativistic self-consistent mean field using the relativistic Hartree-Bogoliubov (RHB) equations 5 ,

where u _n and v _n are Hartree-Bogoliubov wave functions that are corresponding to energy level E _n . The single-nucleon Dirac Hamiltonian h _D is defined as:

The parameters β, effective mass and vector potential are described in detail by the meson-exchange model 5 . The pairing field reads

The index refer to the coordinates in space, spin and isospin. are the matrix elements of two-body pairing interactions. The pp-correlation potentials are the pairing part of the Gorny force D1S 11 . Because the vector potential in Eq. ( 10 ) depends on the nuclear density ρ and the pairing potential in Eq. ( 11 ), our formula relies on pairing tensor κ; thus, it is crucial to define it. For the RHB ground state 5 , it as follows:

In order to determine the nuclear density, we begin by calculating the Dirac Hamiltonian h _D and the pairing field using parameters of the density-dependent meson-exchange relativistic energy functional DD-ME2 6 and of the Gorny force D1S 11 . Then, the Hartree-Bogoliubov wave functions are obtained by solving Eq. ( 9 ), before applying to Eqs. ( 12-13 ) to obtain the nuclear density and pairing tensor. The procedure is repeated until the nuclear density is convergent.

Results

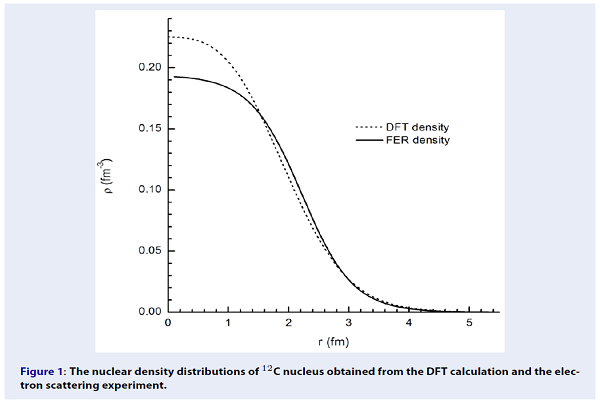
To begin with, nuclear density distributions were calculated by two methods: the electron scattering experiment and the microscopic DFT calculation. In the former method, the two-parameter Fermi distribution was chosen to describe the nuclear density with parameters adjusted to correctly give the experimental value of nuclear rms matter radius (ρ ₀ = 0.194 fm ^-3 , c = 2.214 fm, d = 0.425 fm) 9 . In the latter method, the nuclear density distribution was obtained by the self-consistent mean field calculation, using Eqs. ( 9 )-( 13 ). All the calculations of DFT were performed by the RDIHB program 5 . In Figure 1 , we show these ¹² C density distributions as the function of distance. The dashed line represents the nuclear density calculated from the DFT (called the DFT density), while the solid line is the result of nuclear density obtained from the electron scattering experiment (called the FER density).

Figure 1 . The nuclear density distributions of ¹² C nucleus obtained from the DFT calculation and the electron scattering experiment.

One can see that the DFT reproduces a tight nuclear density distribution in comparison with the Fermi function. As a result, to conserve the nucleon number, the DFT density at the nuclear center is higher about 15% than the FER density. At the surface region, the diffuseness of DFT density distribution is slightly larger than that of FER one, which leads the discrepancy of the nuclear rms matter radii obtained from two methods. In particular, the root-mean-square (rms) of nuclear matter radius was evaluated from DFT (about 2.44 fm) and is larger than the experimental value (about 2.33 fm) 4 . We will consider how these densities affect the nuclear potential.

The calculation of the nuclear folding potential is performed using Eqs. ( 2 )-( 4 ) within a self-consistent procedure. In this work, the effective CDM3Y3 interaction, proven to be successful in the OM analysis of elastic scattering data over a wide range of energies 3 , is used as an input for the folding calculation. Both the DFT and FER density distributions were used in the folding procedure.

Figure 2 . The nuclear potentials of ¹² C+ ¹² C system at the bombarding energy (E _lab = 102.1 MeV) stage corresponding to the DFT and FER density distributions .

The nuclear ¹² C- ¹² C potentials at the bombarding energy of 102.1 MeV using two different density distributions are shown in Figure 2 . The dashed and solid lines describe the folding potentials using two different inputs of DFT and FER density distributions, named P1 and P2, respectively. Both the P1 and P2 potentials have almost similar shapes and depths (about 280-290 MeV). The effective CDM3Y3 interaction depends on the nuclear medium surrounding the two interacting nucleons. Thus, this interaction feels a tight nuclear medium arising from the DFT density in comparison with that of the FER density in the separation; R < 1.5 fm (as seen in Figure 1 ). Therefore, it is reasonable to obtain the P1 potential more shallow than the P2 potential in the deep region, i.e ., R < 1.5 fm.

Now we analyze the elastic ¹² C+ ¹² C scattering data 12 based on the OM with the real part of OP in ( 1 ) and sequentially replaced by the P1 and P2 potentials. In OM analysis, the Coulomb potential, the last term of ( 1 ), is calculated by folding two uniform charge distributions of ¹² C 2 . The Woods-Saxon parameters in (1) are taken from the global OP for the elastic ¹² C+ ¹² C scattering analysis 13 .

A comparison between the theoretical results and the experimental data of elastic ¹² C+ ¹² C angular distributions are shown in Figure 3 . The theoretical evaluation was obtained by OM calculation sequentially using P1 (dashed lines) and P2 (solid lines) potentials. In general, the P2 potential gives a better description of the elastic ¹² C+ ¹² C scattering data than does the P1 potential. However, there are some points at which it has a large deviation from experimental data compared to results of the P1 potential, especially at around 65 degree and 80 degree angles; E _lab =102.1 MeV. At forward angles, although both potentials nearly give the similar results, the P1 tends to be better than the P2 at angles of around 30 degrees. At backward angles, the P1 potential almost describes a wrong shape of angular distributions.

Figure 3 . The elastic angular distributions of ¹² C + ¹² C system at E _lab =102.1, 112 and 121.6 MeV. The data are taken from Ref. 12 .

Discussion

The results of this study provide some information about the DFT. The density of ¹² C which is calculated by the DFT is quite similar to that from the electron scattering experiments at the surface. However, the values in the inner region of both methods are different. This leads to differences in cross sections at large angles. As can be seen in Figure 3 , the DFT is inappropriate to give the angular cross sections at backward angles, and thus, it gives a bad description of the nuclear density of ¹² C in the inner region. There are a few reasons to explain this. One is that the self-consistent mean field tends to be successful in describing the structural properties of medium-heavy and heavy nuclei rather than light ones. It is a rough approximation to consider the light nuclei as a mean field. Another reason is that the parameters of the effective interaction DD-ME2, which is utilized in the DIRHB program 5 , were adjusted to reasonably reproduce the properties of nuclear matter, binding energies and charge radii. Some medium-heavy and heavy nuclei were obtained from the experiments (except ¹⁶ O) 6 . This leads to a poor description of the nuclear density of light nuclei, such as ¹² C, using the effective DD-ME2 interaction.

Conclusions

The OM analysis of elastic ¹² C+ ¹² C scattering data at medium energies has been performed. To illustrate the difference between two nuclear density distributions, the real part of OP was constructed in the framework of the double folding model without free parameters. Besides the chosen effective NN interaction, two density distributions obtained from the elastic scattering experiment and the DFT calculation were used as the independent inputs for the nuclear folding procedure. The analysis shows that DFT gives a bad description of the nuclear density of ¹² C in the interior region, and from the results, it also describes wrong shapes of elastic ¹² C+ ¹² C angular distributions at backward angles in three considered energies. Further studies include investigating the DFT to improve the density calculations for nuclear reaction uses.

Competing Interests

The authors declare that they have no competing interests.

Authors' Contributions

Nguyen Dien Quoc Bao and Le Hoang Chien developed the theoretical formalism, performed the analytic calculations and contributed to the manuscripts. Trinh Hoa Lang and Chau Van Tao reviewed and provided critical feedback.

Acknowledgments

Abbreviations

DFT : Density functional theory

NN : Nucleon-nucleon

OM : Optical model

OP : Optical potential

RHB : Relativistic Hartree-Bogoliubov

rms : Root-mean-square