The Dependence on the Armchair/zigzag Edge Ratio of the Melting Process of Armchair Hexagonal Boron Nitride Nanoribbon

Abstract

The dependence on the armchair/zigzag edge ratios of armchair hexagonal boron nitride nanoribbon (h-BNNR) is investigated by molecular dynamics simulation. To do that, initial configurations with eight different armchair/zigzag edge ratios (0.017377, 0.069510, 0.278481, 0.434782, 1.724409, 6.968254, 10.745098, and 43.88) of armchair h-BNNR containing the same number of atoms (10000 identical atoms of B and N) are heated from 50 K to 7000 K via Tersoff potential. The initial (0.017377 armchair/zigzag ratio) and the final (43.88 armchair/zigzag ratio) configuration strongly affect the melting process of armchair h-BNNR: The 0.017377 armchair/zigzag configuration has a high value of the melting point (5300 K) in comparison to the left seven cases; The melting process of the 43.88 armchair/zigzag ratio configuration is strongly affected by the finite size effects. The melting point of the left six configurations is not affected by the armchair/zigzag edge ratio much and the average value of the melting point for these cases is 4180 K. In the case of 10000 atoms in the configuration, the critical armchair/zigzag edge ratio is found at 10.745098. At this critical armchair/zigzag edge ratio, the melting point fluctuates a bit about 4040 K when the number of atoms in the configuration is increased from 10000 to 25600 atoms. Note that, the melting point of the configuration having this critical armchair/zigzag ratio will not be affected much when the number of atoms in the configuration is increased.

INTRODUCTION

The remarkable properties of two-dimensional materials have garnered considerable attention in recent years, owing to their unique electronic, thermal, and mechanical characteristics. Graphene, a single layer of carbon atoms arranged in a hexagonal lattice, has emerged as a revolutionary material with extraordinary properties, revolutionizing the landscape of materials science and technology 1 . Beyond graphene, a rich family of two-dimensional materials, often referred to as "graphene-like" materials, has been discovered, each with its own unique characteristics and applications. Materials such as hexagonal boron nitride (h-BN) 2 , 3 , 4 , 5 , transition metal dichalcogenides 6 , 7 , and black phosphorus (phosphorene) 8 , 9 are among the graphene-like materials that have garnered attention for their unique properties. h-BN, for instance, is an insulator with excellent thermal stability, serving as an ideal substrate for graphene-based devices 5 , 10 , 11 , 12 , 13 . Armchair hexagonal boron nitride nanoribbons (h-BNNR) are narrow strips of h-BN with specific edge configurations that can be tailored to exhibit distinct electronic behaviors 14 , 15 , 16 . Therefore, armchair h-BNNR stands out as a promising candidate due to its intriguing combination of properties.

The thermal properties of armchair h-BNNR are not only of fundamental interest but also hold significant practical implications for nanoelectronics 17 , thermal management 18 , and materials science. As the width of these nanoribbons is reduced towards the nanoscale, quantum size effects become increasingly pronounced, resulting in unique thermal behaviors 19 , 20 . Additionally, the specific edge configurations, whether zigzag or armchair, can have a profound impact on their thermal properties 11 , 21 , 22 . This influence stems from the altered phonon dynamics, lattice vibrations, and thermal transport mechanisms at the edges of the ribbons.

Up to now, the implementation of the armchair h-BN melting process has encountered many challenges. However, experimental results have been obtained for h-BN in powder form. Powder h-BN has a high melting point, typically around 3000°C (depending on the purity and crystalline structure) 23 . This high melting point is due to the strong covalent bonds between boron and nitrogen atoms, similar to those in diamond and graphite in carbon-based materials.

Understanding the interplay between size, edge structure, and thermal behavior in armchair h-BNNR is not only essential for fundamental insights into nanoscale heat transport but also holds the potential for the design of advanced nanomaterials with tailored thermal characteristics for diverse technological applications. In this study, by using molecular dynamics (MD) simulation, we delve into the dependence of the melting process of armchair h-BNNR on the armchair/zigzag (A/Z) ratio and define the critical A/Z ratio. Note that the melting point of the configuration having this critical A/Z ratio will not be significantly affected when the number of atoms in the configuration is increased. Details on the calculation are given in Section 2. Results and discussion are shown in Section 3. Conclusions are presented in the last section of the paper.

CALCULATION

One of the critical aspects of MD simulations is the choice of interatomic potential functions, which govern the interactions between particles in the simulated system. Among these potential functions, the Tersoff potential stands out as a versatile and widely used model, particularly in the study of covalent and semi-covalent materials. Unlike simple pairwise potentials like Lennard-Jones, the Tersoff potential offers a more sophisticated description of bond-breaking and bond-forming events, capturing the intricacies of chemical bonding and the structural changes that occur during the simulation.

This potential model is particularly adept at reproducing key material properties, including the prediction of lattice constants, elastic constants, phonon spectra, and defect energetics. Moreover, it excels in simulating complex phenomena like dislocations, chemical reactions, and the mechanical behavior of materials under extreme conditions. The Tersoff potential's flexibility and versatility stem from its parametrization, which allows researchers to tailor the potential parameters to specific materials and applications.

In this study, the interactions between and in the initial configurations are described by Tersoff potential 24 which is written as below:

Here, is the distance from atom i to atom j. The repulsive and the attractive terms are based on Morse potential as proposed by Brenner 25 . The cutoff function using for calculating the number of neighbors as well as making the potential to zero outside the interaction shell is term.

We use the software package Large-Scale Atomic/Molecular Massively Parallel Simulator to perform the MD simulation 26 . The ISAACS software is used to calculate some thermal quantities 27 . To visualize the atomic configuration, we use VMD software 28 . The temperature inscreases as: , in which, K is the initial value of temperature of the simulation, is a heating rate, and t is the time required for heating. Note that, the heating rate in this study is K/s. To study the structural characteristics at given temperatures, configurations are relaxed for MD steps (0.0001 picoseconds per step) to ensure the configuration stability.

To study the dependence on the A/Z edge ratio of h-BNNR melting process, all initial armchair h-BNNR configurations have to be the same number of atoms (10,000 atoms) but differ in zigzag- and armchair-edge lengths. To keep the number of atoms of the initial configurations being 10,000 atoms, we have to adjust the length of the armchair and zigzag edges as shown in Table 1 .

Table 1 The zigzag- and armchair-edge lengths of the armchair h-BNNR.

The simulation passes some stages below:

i) To ensure the configuration stability, the initial configurations are relaxed for MD steps at 50 K under periodic boundary conditions using canonical ensemble simulation

ii) To have armchair h-BNNR, non-periodic boundary conditions with an elastic reflection behavior are applied along the zigzag edges after adding a space of 20 Å at both ends. After that, initial configuration are relaxed again to equilibrium further for MD steps at 50 K using canonical ensemble simulation

iii) The configurations are heated up to about 7000 K which is higher than the melting point of zigzag h-BNNR 11 to ensure that at the chosen temperature (7000 K) all configurations are in a liquid state.

RESULTS AND DISCUSSION

To study the thermodynamic properties of materials upon heating, the total energy per atom plays a crucial role which helps in understanding how a material responds to changes in temperature. Based on the total energy per atom one can observe the phase transitions and the temperature at the phase transitions such as melting point. In this study, to investigate the influence of armchair and zigzag edges on the melting process of armchair h-BNNR the total energy per atom of eight configurations in Table 1 is calculated and presented in Figure 1 .

Based on the results of the total energy per atom (square symbol in Figure 1 ) one can see that except for Configuration 8 in Table 1 (square symbol in Figure 1 h), the graphs of the total energy per atom of the other configurations in Table 1 (square symbol in Figure 1 a-g) divide into two regions: i) In the first region, the graph of the total energy per atom for each configuration increases linearly to a certain value of temperature. This indicates that the configurations are in a crystal state. At this state, the atoms in the configurations oscillate about their equilibrium positions but these amplitudes of the vibration are not big enough to break the bonds between atoms. Therefore, the materials are still in a crystal state; ii) Upon heating further, there is a sudden jump in the total energy per atom to a higher energy region. This behaviour of the total energy shows the phase transition often referred to as a first-order phase transition which is characterized by a sudden and discontinuous change in total energy per atom.

Related to Configuration 8 in Table 1 , the behavior of the total energy per atom does not follow any rule maybe due to the strong effect of the edge size on the melting process of the configuration leading to the finite size effects.

Figure 1 . Total energy per atom (square symbol) and heat capacity (solid line) of armchair h-BNNR configurations containing 10,000 atoms in Table 1: a) Configuration 1: A/Z ratio is 0.017377, b) Configuration 2: A/Z ratio is 0.069510, c) Configuration 3: A/Z ratio is 0.278481, d) Configuration 4: A/Z ratio is 0.434782, e) Configuration 5: A/Z ratio is 1.724409, f) Configuration 6: A/Z ratio is 6.968254, and g) Configuration 7: A/Z ratio is 10.745098, h) Configuration 8: A/Z ratio is 43.88.

One can see that the initial configurations are in a crystal state. When these initial configurations are heated, the temperature in these configurations increases until these configurations reach their melting point. At the melting point, these configurations start to absorb heat energy to undergo the phase transition into a liquid state while the temperature remains constant until the entire crystal structure has melted. After that, the temperature in these configurations increases again. So, the change of the heat with respect to the temperature (the heat capacity) shows a peak at the melting point (the phase transition temperature). In general, the heat capacity is defined as below:

In which, E is the total energy per atom, and T is temperature. In this context, the peak of the heat capacity can be used to define the melting point of the configurations.

The heat capacity of eight configurations in Table 1 is calculated based on the total energy and is shown in Figure 1 (solid line). The melting point of every configuration is defined at the peak of the heat capacity line and presented in Table 2 .

Table 2 The melting point of different A/Z edge ratios of armchair h-BNNR configurations containing 10,000 atoms.

Based on the results in Table 2 , we can point out the following key points:

i) As for Configuration 1 in Table 1 (0.0173770 A/Z edge ratio), the melting temperature (5300 K) is higher than the other ones ( Table 2 , Figure 1 a). Meanwhile, regarding Configuration 8 in Table 1 (43.88 A/Z edge ratio), the phase transition is complicated due to the influence of finite size effects ( Figure 1 h). The main reason here is the length of the armchair edges between configurations 1 and 8 in Table 1 . The armchair length in Configuration 1 (0.0173770 A/Z edge ratio) is too short compared to the zigzag edge. As well known, compared to the zigzag edges, the armchair edges contain more dangling bonds which are unstable. This results in the armchair edges being more susceptible to external factors than the zigzag edges. Therefore, in Configuration 1 in Table 1 , the length of the armchair edge is much shorter than the zigzag edge, leading to a high melting temperature in the configuration. However, in Configuration 8 in Table 1 (43.88 A/Z edge ratio), the A/Z edge ratio is 43.88, proving that the armchair edge length is nearly 44 times longer than the zigzag one, leading to finite size effects in the melting process. Thus, to have a general view of the influence of armchair and zigzag edge lengths, other A/Z ratios are larger than the one of Configuration 1 (0.0173770) and smaller than the one of Configuration 8 (43.88) ( Table 1 ). This means that we need to consider Configurations 2 to 7 in Table 1 .

ii) Related to Configurations 2 to 7 in Table 1 , the A/Z edge ratios range from 0.069510 to 10.745098. Within this range of A/Z edge ratio, the melting temperature point varies from 3900 to 4300 K ( Figure 1 , Table 2 ). On average, the melting temperature within this ratio range is approximately 4180 K. It can be observed that the A/Z edge ratio does not significantly affect the melting temperature within this range. Specifically, Configuration 2 (0.06951 A/Z edge ratio) and Configuration 7 (10.745098 A/Z edge ratio) in Table 1 both exhibit a melting temperature of 4200 K ( Table 2 ). However, the total energy per atom of Configuration 7 is higher than Configuration 2 ( Figure 2 ). This may be because Configuration 7 has a longer armchair edge length than Configuration 2, leading to the total energy per atom being higher (Tables 1 and 2, Figure 2 ). Thus, the melting temperature point of these two configurations (2 and 7) only differs very slightly from the average temperature point of the left six configurations in Table 1 (from 2 to 7): 4200 K versus 4180 K. Therefore, it is necessary to investigate these two A/Z edge ratios to find a critical A/Z edge ratio. Note that, the melting point of the configuration having this critical A/Z edge ratio will not be affected much when the number of atoms in the configuration is increased.

Figure 2 . Total energy per atom of armchair h-BNNR configurations containing 10,000 atoms: Configuration 2 in Table 1 (0.069510 A/Z edge ratio) – square symbols and Configuration 7 in Table 1 (10.745098 A/Z edge ratio) – circle symbols.

First, for Configuration 2 in Table 1 (A/Z ratio of 0.06951), the number of atoms in the configuration is increased from 10,000 atoms to 14,400, 19,600, and 25,600 atoms, but the A/Z ratio remains the same. Results from the graph of total energy per atom show that all of these configurations exhibit first-type phase transition ( Figure 3 ). The phase transition temperatures of the 10,000, 14,400, 19,600, and 25,600 -atom configurations are 4200, 3730, 3630, and 3520 K, respectively. One can see that although the difference in the number of atoms between configurations is about 5000 atoms, there is only a big difference in the phase transition temperature point of the 10,000-atom configuration (4200 K) compared to the 14,400, 19,600, and 25,600 -atom configurations (3730, 3630, and 3520 K, respectively). The phase transition temperature points of the left three configurations (14,400, 19,600, and 25,600 atoms) do not fluctuate much even though the gap in the number of atoms between configurations is also 5000 atoms. Therefore, within the scope of this study, it can be concluded that the phase transition temperature point of the configurations having 0.06951 A/Z ratio is just relatively stable when the number of atoms in the configuration is from 14,400 to 25,600.

Figure 3 . Total energy per atom of armchair h-BNNR configurations with 0.06951 A/Z ratio: 10,000 atoms – square symbols, 14,400 atoms – circle symbols, 19,600 atoms –triangle symbols, and 25,600 atoms – star symbols.

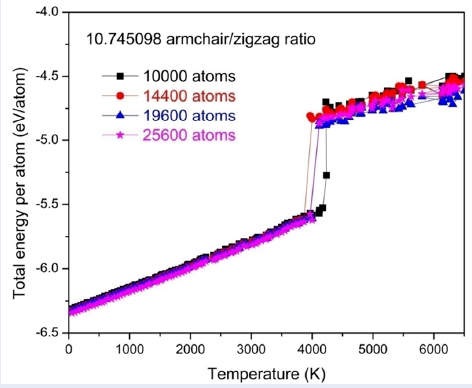
As for Configuration 7 in Table 1 (10.745098 A/Z ratio), the number of atoms in the configuration also increases from 10,000 atoms to 14,400, 19,600, and 25,600 atoms but the A/Z ratio remains the same (10.745098). The melting temperature points of the 10,000, 14,400, 19,600, and 25,600-atom configurations are 4200, 3940, 4040, and 4040 K, respectively ( Figure 4 ). This means that the melting temperature point of the 10.745098 A/Z case is not affected much by the number of atoms in the configuration even in case of 10,000 atoms ( Figure 4 ). In particular, the melting temperature points of 19,600 and 25,600 -atom configurations are the same as shown in Figure 4 (4040 K). It can be concluded that in the case of the 10.745098 A/Z ratio, the number of 10,000 atoms in the configuration has relatively ensured the stability of the phase transition temperature point. In addition, the noise of total energy in the 10.745098 A/Z configuration is less perturbed than the case of 0.06951 A/Z one ( Figure 3 , Figure 4 ). The reason may be due to the armchair edge length in the case of 10.745098 A/Z ratio being large ( Table 1 ).

Figure 4 . Total energy per atom of armchair h-BNNR configurations with 10.745098 A/Z ratio: 10,000 atoms – square symbols, 14,400 atoms – circle symbols, 19,600 atoms – triangle symbols, and 25,600 atoms – star symbols.

Thus, within the scope of this study, in the case of the 10.745098 A/Z ratio, the configuration containing 10,000 atoms is large enough to ensure the relative stability of the phase transition temperature zone. Therefore, the 10.745098 A/Z ratio can be considered the critical A/Z edge ratio. The 10.745098 A/Z configuration can be visually observed before the melting temperature point ( Figure 5 a) and at the melting temperature point ( Figure 5 b).

Figure 5 . Three-dimensional view of armchair h-BNNR configuration having 10.745098 A/Z ratio at different values of temperature: a) 3000 K, b) 4200 K.

In addition to Configuration 8 in Table 1 (43.88 A/Z ratio), several visualizations at different temperatures are shown to easily visualize the finite size effects. Based on the peaks in the heat capacity graph (solid line in Figure 1h), several temperature values are chosen and presented in Figure 6 . One can see that the crystal structures in this configuration break at a much lower temperature than those in the remaining configurations in Table 1 due to the finite size effects ( Figure 6 ).

Figure 6 . Three-dimensional view of armchair h-BNNR configuration having 43.88 A/Z ratio at different values of temperature: a) 2500 K, b) 4200 K, and c) 5400 K.

CONCLUSION

The melting process of armchair h-BNNR configuration containing 10,000 atoms is performed with different A/Z ratios to study the dependence of the melting process on the length of the armchair edges and to find the critical A/Z ratio. The Tersoff potential is applied to the interactions between B and N.

- To consider the dependence on A/Z ratios, eight different A/Z ratio configurations (0.017377, 0.069510, 0.278481, 0.434782, 1.724409, 6.968254, 10.745098, and 43.88) of armchair h-BNNR configuration containing the same number of atoms (10,000 atoms) are studied. The results show that the melting process is strongly affected by the configurations with 0.017377 and 43.88 A/Z ratios. The former has a melting point of 5300 K while the latter is affected by the finite size effects. Related to the other configurations, the average value of melting point is 4180 K. And two of them (0.069510 and 10.745098 A/Z ratios) are chosen to find the critical A/Z ratio because these two configurations have the same value of melting point (4200 K) which is closed to the average melting point (4180 K). Note that, the melting point of the configuration with this critical A/Z edge ratio will not be affected much when the number of atoms in the configuration is increased.

- To find the critical A/Z ratio, the A/Z ratios of the two chosen configurations are fixed but the number of atoms in the configuration is increased from 10,000 to 14,400, 19,600, and 25,600 atoms for both 0.069510 and 10.745098 A/Z cases. The results show that the 10.745098 A/Z ratio can be considered the critical A/Z edge ratio because its melting point is not affected much when the number of atoms is increased. In addition, the total energy of the 10.745098 A/Z ratio is less noisy than the one of 0.069510 cases because long the length of the armchair edges.

- The found critical A/Z ratio in this study can be the benchmark for further experimental and theoretical studies.

Abbreviations

armchair/zigzag (A/Z); hexagonal boron nitride (h-BN); hexagonal boron nitride nanoribbon (h-BNNR); molecular dynamics (MD)

Acknowledgments

We acknowledge Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for supporting this study.

Author’s contributions

Hang T. T. Nguyen conceived of the presented idea, performed the computations, analyzed the data, supervised the findings of this work, and wrote the manuscript.

Funding

None.

Availability of data and materials

Not applicable.

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.