Open Access 
Abstract
Introduction: In this study, we investigate how boundary conditions influence the structural evolution of hexagonal boron nitride (h-BN) under thermal stress. Specifically, we analyze two configurations: a zigzag h-BN nanoribbon (ZBNNR) and an in-plane graphene/h-BN/graphene (g/h-BN/g) heterostructure, focusing on the role of graphene layers in modulating h-BN's behavior during heating.
Methods: Molecular dynamics simulations were employed to simulate thermal effects on the ZBNNR and hybrid g/h-BN/g heterostructure. These simulations tracked structural changes, bond dynamics, and phase transitions across varying temperatures to assess boundary-driven modifications in h-BN stability.
Results: Both systems exhibited first-order phase transitions. The melting temperature of ZBNNR was 3800 K, significantly lower than the 6150 K observed for the g/h-BN/g heterostructure. At melting, B–B and N–N bonds in ZBNNR contracted, whereas these bonds remained stable in the heterostructure. Coordination analysis revealed that 5.9% of atoms in ZBNNR retained a coordination number of three, compared to only 2.6% in the h-BN layer of the heterostructure, highlighting graphene’s stabilizing effect.
Conclusion: The presence of graphene layers in the hybrid heterostructure substantially enhances the thermal stability of h-BN, elevating its melting temperature and suppressing bond distortion. This work underscores the critical role of boundary conditions in tailoring nanoscale material properties for high-temperature applications.
INTRODUCTION
Graphene, a single layer of carbon atoms arranged in a hexagonal lattice, is renowned for its exceptional mechanical strength, high electrical conductivity, and remarkable thermal properties 1 . In contrast, h-BN consists of alternating boron and nitrogen atoms in a similar hexagonal lattice structure, offering excellent insulating behavior, thermal stability, and a wide bandgap 2 , 3 . Both graphene and h-BN have been synthesized experimentally. In contrast to the hexagonal configuration of graphene nucleation islands, h-BN initiates growth with a triangular shape, potentially influenced by the higher energy preference of nitrogen-terminated edges 4 . h-BN can exist in different structural forms, including armchair and zigzag configurations, which refer to the arrangement of the lattice. Both armchair and zigzag types of h-BN share the fundamental properties of high thermal stability and excellent insulating properties 5 , 6 , 7 .
When graphene and h-BN layers are stacked together in a van der Waals (vdW) heterostructure, they create a unique material system with enhanced properties. The precise stacking arrangement, often achieved in the Bernal stacking configuration, forms a moiré superlattice with a longer periodicity 8 , 9 . This moiré pattern leads to spatially modulated electronic and optical properties, giving rise to various phenomena and functionalities 10 , 11 . Moreover, the combination of the high electrical conductivity of graphene with the insulating behavior of h-BN makes vdW graphene/h-BN heterostructures promising candidates for various applications in electronics 12 , 13 , optoelectronics 14 , and thermal management 15 . One of the outstanding applications of vdW graphene/h-BN is as a field-effect tunneling transistor, which represents a promising class of electronic devices with the potential to address key challenges in energy efficiency, speed, size, and functionality in future electronic systems 12 . In parallel with studies on the electrical properties of vdW graphene/h-BN, the thermal conductivity properties were also investigated in detail because of significant interest in their implications for thermal management in nanoelectronic devices and related applications 16 , 17 . In addition to the vdW heterostructure, there is also an in-plane hybrid graphene/h-BN/graphene heterostructure. This heterostructure can have several intriguing properties and potential applications because of the combination of the electronic properties of graphene and the insulating and structural properties of h-BN 18 , 19 , 20 .
To provide more information about the influence of the boundary conditions on the melting process of the h-BN sheet, molecular dynamics (MD) simulations were performed. The results of MD simulations can shed light on phase transitions and thermal properties, providing insights into phenomena such as the melting point and phase transformation. Details on the calculation are presented in Section 2. The results can be found in Section 3. The discussion is presented in Section 4. Conclusions are given in the last section of the paper.
CALCULATION
The role of the interaction potential is critical in MD simulations, as it governs how particles behave and move within the simulated system. In MD simulations, a key aim is to accurately replicate real-world interactions between atoms or molecules in a computationally feasible way. The interaction potential encompasses the forces and energies of various atomic interactions, including bonded and nonbonded interactions. In systems with covalent bonds, where chemical bonds connect atoms, the interaction potential dictates the stretching, bending, and torsional forces that occur as atoms undergo movement and rearrangement. This capability allows the simulation to accurately depict processes such as bond breaking and formation, which is essential for studying chemical reactions and structural transitions. Various empirical potentials, including those representing two- and three-body interactions in different forms, are available 21 , 22 , 23 , 24 . The Tersoff potential specifically addresses the interatomic forces and energies involved in covalent bonding in materials, making them highly suitable for studying systems characterized by strong chemical interactions 25 , 26 , 27 . What distinguishes the Tersoff potential is its ability to model complex phenomena such as bond breaking and reformation, anisotropic and directional bonding, and interactions at both short and long ranges. This broad representation extends their usefulness from basic elements such as carbon to a diverse range of covalent materials such as semiconductors and heterostructures.
In this study, the Tersoff potential 28 is used for the interactions between B, N, and C in the initial configurations, which are written as follows:
where r ij is the distance from atom i to atom j. The repulsive f R (r ij ) and the attractive f a (r ij ) terms are based on the Morse potential, as proposed by Brenner 29 . The f c (r ij ) term represents the cutoff function used for calculating the number of neighbors and making the potential zero outside the interaction shell. To perform the calculations, the software package Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) is used 30 .
First, the lengths of the zigzag and armchair edges as well as the number of atoms in the initial h-BN configuration are determined on the basis of a previous study on the influence of the armchair/zigzag edge ratio on the melting process of free-standing h-BN 31 . Accordingly, the configuration with an armchair/zigzag edge ratio of 10.745098 and 25600 atoms is selected for investigation in this study. The influence of boundary conditions on the evolution of the h-BN layer structure upon heating can then be observed through the investigation of the following two cases:
i) Influence of the nonperiodic boundaries along the armchair direction on the melting process of h-BN
First, the h-BN configuration is relaxed in the NVT ensemble to achieve an equilibrium state under periodic conditions along the zigzag and armchair edges. Then, the armchair directions are fixed after adding a space of 10 Å, whereas the zigzag directions are still under periodic conditions. A material with similar profiles is called a zigzag h-BN nanoribbon (ZBNNR), as shown in Figure 1 . Next, the configuration with new boundary conditions is relaxed again for the 6x10 5 MD steps. Finally, the h-BN sheet is heated from 300 K to 7000 K to ensure that the configuration is liquid. Note that the ZBNNR configurations containing 25600 32 and 10000 6 atoms with other armchair/zigzag edge ratios are examined.
Figure 1 . The initial ZBNNR configuration .The boron and nitrogen atoms are colored ochre and blue, respectively.
ii) Influence of the graphene layers on the melting process of h-BN in the in-plane hybrid graphene/h-BN/graphene (g/h-BN/g) heterostructure
In this case, the h-BN configuration will be hybridized with graphene at the two zigzag edges to make the armchair directions nonperiodic, as shown in Figure 2 . Note that to choose the number of atoms for the graphene layer, several cases have been performed, and we found that the melting process of the hybrid g/h-BN/g heterostructure depends on the graphene/h-BN atomic ratio, which has also been confirmed in some previous papers 19 , 31 , 33 . For this study, we choose 32600 atoms in each graphene layer. Then, the hybrid in-plane graphene/h-BN/graphene configuration is relaxed again for 6x10 5 the MD steps. Finally, the hybrid graphene/h-BN/graphene configuration is heated from 300 K to 7000 K to ensure that the graphene/h-BN/graphene configuration is in a liquid state.
Figure 2 . Initial in-plane g/h-BN/g heterostructure . Boron, nitrogen, and carbon atoms are colored in order of ochre, blue, and cyan, respectively.
The change in the temperature upon heating in the two cases obeys T 0 + vt, where T 0 = 50K, v is the heating rate (5x10 12 K/s), and t is the time required for heating. All configurations at the chosen temperatures are relaxed for 6x10 5 MD to ensure configuration stability before the structural evolution or 2D visualization is studied. The interval of time for every single step is 0.0001 picoseconds. We use VMD software to visualize the atomic configurations 34 .
RESULTS
In this section, we present some computational results to show the influence of boundary conditions on the melting process of ZBNNR. We begin by examining the energy change upon heating. The phase transition temperature region can be defined on the basis of the total energy per atom of the configuration upon heating. In this situation, the total energy is the sum of various energy contributions, including kinetic energy (associated with atomic motion) and potential energy (associated with interatomic interactions). In a crystalline state, atoms are arranged in a highly ordered lattice structure, with relatively low kinetic energy and stable interatomic interactions. Upon heating, the particles rearrange, and the lattice structure breaks down, increasing the degree of atomic motion and interatomic distance changes. As more energy is required to overcome interatomic forces and facilitate particle motion, the phase transitions from a crystalline state to a liquid state. The total energy per atom of the ZBNNR and in-plane g/h-BN/g configurations are plotted in Figure 3 (square symbol – ZBNNR and circle symbol – g/h-BN/g).
Figure 3 . The total energy per atom upon heating: square symbol, ZBNNR configuration; circle symbol, g/h-BN/g heterostructure.
To define the melting point, the heat capacity is applied via the following formula:
where E is the total energy and T is the temperature. The heat capacities of the ZBNNR and g/h-BN/g configurations are calculated and presented in Figure 4 (square symbol – ZBNNR configuration; circle symbol – g/h-BN/g heterostructure). The heat capacity represents the amount of energy needed to increase the temperature of a substance by a certain amount. Following that, the heat capacity peaks at the melting point at which the total energy increases sharply.
Figure 4 . The heat capacity upon heating: square symbol – ZBNNR configuration, circle symbol – g/h-BN/g heterostructure .
To visualize the ZBNNR and g/h-BN/g configurations at the melting point, a three-dimensional view of the configurations is presented in Figure 5 .
Figure 5 . Three-dimensional view of the configurations at the melting point: a) ZBNNR at the melting point of 3800 K and b) g/h-BN/g at the melting point of 6150 K.
To study the influence of the boundary conditions on the atomic evolution upon heating, several quantities, such as the radial distribution function, the coordination number, the angular distribution, and the bond length, are calculated for the case of ZBNNR and the h-BN layer in the hybrid g/h-BN/g heterostructure.
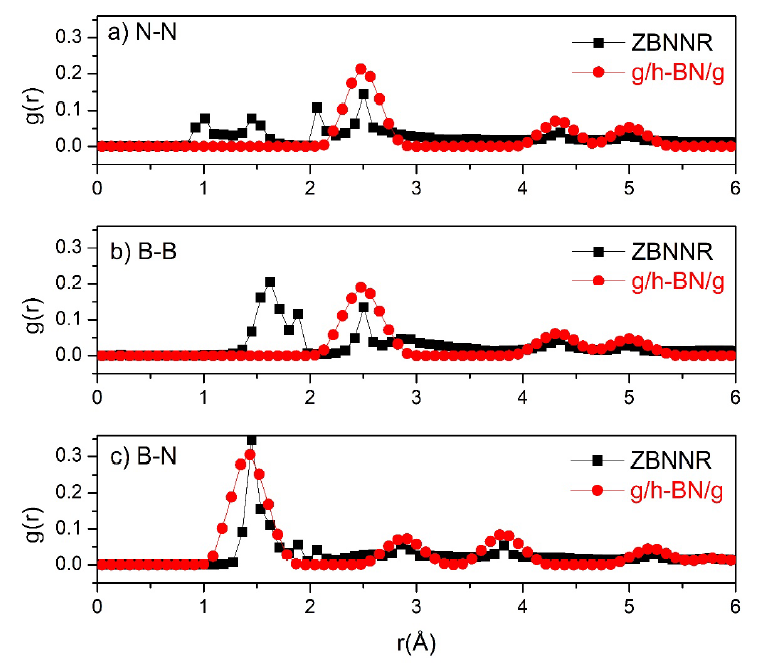
The radial distribution functions g(r) of the ZBNNR configuration (square symbol in Figure 6 ) and the h-BN layer in the hybrid g/h-BN/g heterostructure (circle symbol in Figure 6 ) at the melting point are calculated as shown in Figure 6 .
Figure 6 . Radial distribution functions g(r) of the ZBNNR configuration (square symbol) and the h-BN layer in the hybrid g/h-BN/g heterostructure (circle symbol) at the melting point: a) N‒N, b) B‒B, and c) B‒N .
The atomic mechanism of the melting process from a crystal to a liquid state involves several criteria, such as the radial distribution function, which is a concept used to predict the change in position of atoms in the configuration on the basis of the distribution of atoms in the configuration. The radial distribution function g(r) is defined as follows:
in which is a function that computes the number of atoms within a shell of thickness , and the average density at any point is ρ.
Figure 7 . The formation of different coordination numbers surrounding B in the case of ZBNNR and h-BN in the hybrid g/h-BN/g heterostructure upon heating: empty column – ZBNNR, solid column – h-BN in the hybrid g/h-BN/g heterostructure .
In this study, the environments (number of N atoms) for B atoms are considered. In the crystal state of the ZBNNR and h-BN layers, the number of N atoms surrounding the B atom is three (coordination number of three), except for the case at the boundaries. Therefore, in the crystalline state, the coordination number of three is nearly 100%. Upon heating, the bonds between N and B atoms are broken, leading to the appearance of other coordination numbers, such as two, one, and zero, as shown in Figure 7 .
Figure 8 . Angular distributions in the liquid state: circle symbol - the free-standing h-BN configuration (5050 K), square symbol - h-BN layer in the in-plane hybrid g/h-BN/g heterostructure (4050 K) .
The angular distribution captures the distribution of angles formed by neighboring particles around a central particle. Tracking the evolution of angular distributions allows us to quantify the loss of structural order and the distorted structures.
DISCUSSIONS
The behavior of the total energy per atom of both the ZBNNR configuration (square symbol in Figure 3 ) and g/h-BN/g (circle symbol in Figure 3 ) upon heating can be divided into three parts. First, the total energy per atom increases linearly. This means that atoms are held in fixed positions or oscillate slightly around their equilibrium positions due to interatomic forces. In this situation, the configuration is in a crystalline state. Then, there is a sharp increase in total energy per atom: approximately 3800 K for ZBNNR (square symbol in Figure 3 ) and from 5950 K to 6150 K for g/h-BN/g (circle symbol in Figure 3 ). As the thermal energy increases due to increasing temperature, atoms start to oscillate more vigorously around their equilibrium positions and overcome the forces holding atoms in the crystal lattice. The bonds between neighboring atoms begin to break, leading to a phase transition from a crystalline state to a liquid state. Finally, in the last part of the graph, the total energy per atom again exhibits linear behavior, indicating that the configuration is liquid. One can see that the phase transition from the crystal to a liquid state is of the first-order type.
The heat capacity is used to define the melting point of the configurations. For the ZBNNR configuration, the heat capacity peaks at 3800 K, which represents the melting point (square symbol in Figure 4 ). Note that to date, the experimental melting process of the ZBNNR configuration has encountered many challenges, so there are no experimental results on the melting temperature. However, researchers have previously conducted experiments on h-BN powder and determined that the melting temperature of h-BN powder is approximately 3000 K 35 . This will be the benchmark for simulation studies. With respect to the g/h-BN/g heterostructure, the heat capacity peak is at 6150 K. Note that the melting point of free-standing graphene is approximately 7750 K 36 .
When graphene layers are added to the h-BN nanoribbon to form the in-plane g/h-BN/g heterostructure, the interactions between the B and N atoms of h-BN and the C atoms of the graphene layers can help stabilize the h-BN structure. These interactions can effectively reduce the reactivity of h-BN, increasing the energy required to break bonds in h-BN, thus increasing the melting point of the h-BN layer in the in-plane g/h-BN/g heterostructure in comparison to ZBNNR. This also leads to differences in the structural evolution of the ZBNNR and the h-BN in the in-plane g/h-BN/g heterostructure, which is considered on the basis of the radial distribution functions, the coordination number, and the angular distribution functions.
In this study, the g(r) values of the ZBNNR configuration and the h-BN layer in the hybrid g/h-BN/g heterostructure at the melting point are presented in Figure 6 . For the case of N–N and B–B bonds (Figures 6, a, b), at the melting temperature, these bonds in the ZBNNR configuration tend to shrink (square symbols in Figures 6 a, b). Especially in the case of B-B bonds, the bond length decreases and is most concentrated at the 1.62 Å position, as shown in Figure 6 b (square symbol). Moreover, the bond lengths of N‒N and B-B of the h-BN layer in the hybrid g/h-BN/g heterostructure at the phase transition temperature do not tend to shrink (circle symbols in Figure 6 a, b). For the B-N bond shown in Figure 6 c, the bond lengths of both ZBNNR and h-BN in the hybrid g/h-BN/g heterostructure do not shrink; however, the second and third peaks of the ZBNNR case are lower than those of h-BN in the hybrid g/h-BN/g heterostructure. Compared with the scenario in which the graphene layer is absent, the impact of the graphene layer on the melting process of the h-BN layer can thus be demonstrated. This influence can be observed through the coordination number, as shown in Figure 7 .
For ZBNNR (empty column in Figure 7 ), at the melting point, the coordination number of three decreases significantly to ~5.9% (empty column in Figure 7 ). This leads to the appearance/growth of the coordination numbers of two (~9.8%), one (~22.3%), and zero (~62%) (empty column in Figure 7 ). In particular, the significant increase in the coordination number of zero indicates the existence of B gas at the melting point. With respect to the h-BN layer in the hybrid g/h-BN/g heterostructure, at the melting point, the coordination number decreases significantly to ~2.6% (solid column in Figure 7 ). This leads to the appearance/growth of the coordination numbers of two (~33.6%), one (~54%), and zero (~9.9%) (solid column in Figure 7 ). In particular, the significant increase in the coordination number of one indicates the influence of the graphene layers on the structural evolution of h-BN upon heating in comparison to the ZBNNR case ( Figure 7 ). Note that at the melting point, there is still a coordination number of three (~5.9% for the ZBNNR and ~2.6% for the h-BN in the hybrid g/h-BN/g heterostructure), indicating that there is still some crystalline structure at the melting temperature. This can be verified by examining the angular distribution in Figure 8 .
In the case of the ZBNNR, at the melting point, approximately 39% is at 120 o (square symbol in Figure 8 ). With respect to the h-BN layer in the hybrid g/h-BN/g heterostructure, at the melting point, the angular distribution at 120 o is nearly 6.5%, indicating the collapse of most of the crystal structures (circle symbols in Figure 8 ).
CONCLUSIONS
The influence of boundary conditions on the structural evolution of h-BN upon heating is studied via MD simulations in two cases: the ZBNNR configuration and the h-BN layer in the in-plane hybrid g/h-BN/g heterostructure. One can conclude that the graphene layers strongly affect the structural evolution of the h-BN layer upon heating. Some key points of the study are as follows:
i) The phase transition of both the ZBNNR configuration and the hybrid g/h-BN/g heterostructure is of the first-order kind. The melting temperature point in the case of the ZBNNR configuration is 3800 K, and that of the hybrid g/h-BN/g heterostructure is 6150 K.
ii) At the melting point, some results are as follows: the N‒N and B-B bonds in the case of ZBNNR tend to shrink, whereas those in the case of the h-BN layer in the hybrid g/h-BN/g heterostructure do not; there is still a coordination number of three, but the case of the ZBNNR is ~5.9%, whereas the case of the h-BN layer in the hybrid g/h-BN/g is only ~2.6%.
Competing interests
The authors declare that they have no competing interests.
Author’s contributions
Hang T. T. Nguyen conceived of the presented idea, performed the computations, analyzed the data, supervised the findings of this work, and wrote and submitted the manuscript. Tran Van Luong analyzed the data, wrote the manuscript. All authors read and approved the final manuscript.
Funding
This research is funded by Ho Chi Minh City University of Technology –VNU-HCM, under grant number T-KHUD-2024-03.
Availability of data and materials
Data will be made available on request.
References
- Geim A K. Nobel Lecture: Random walk to graphene. Rev. Mod. Phys. 2011;83:. Google Scholar
- Peng Q, Ji W, De S. Mechanical properties of the hexagonal boron nitride monolayer: Ab initio study. Com. Mat. Sci. 2012;56:11-11. Google Scholar
- Odlyzko M L, Mkhoyan K A. Identifying hexagonal boron nitride monolayers by transmission electron microscopy. Microsc. and Microanal. 2012;18:. Google Scholar
- Kim K K, Hsu A, Jia X, Kim S M, Shi Y, Hofmann M, Nezich D, Rodriguez-Nieva J F, Dresselhaus M, Palacios T. Synthesis of monolayer hexagonal boron nitride on Cu foil using chemical vapor deposition. Nano Lett. 2012;12:161-161. Google Scholar
- Hang N T T. Evolution of Boron Nitride Structure upon Heating. Commun. Phys. 2017;27:301-301. Google Scholar
- Nguyen H T, Hanh T T T. Melting process of zigzag boron nitride nanoribbon. Physica E Low Dimens. Syst. Nanostruct. 2019;106:. Google Scholar
- Nguyen H T T, Luong Tran Van, Ngo T T. Size dependence of melting process of armchair hexagonal boron nitride nanoribbon. Commun. Phys. 2024;34:151-151. Google Scholar
- Yuan L, Li Z, Yang J, Hou J G. Diamondization of chemically functionalized graphene and graphene-BN bilayers. Phys. Chem. Chem. Phys. 2012;14:8179-8179. Google Scholar
- Rothstein A, Schattauer C, Dolleman R J, Trellenkamp S, Lentz F, Watanabe K, Taniguchi T, Kennes D M, Beschoten B, Stampfer C. Band gap formation in commensurate twisted bilayer graphene/hBN moiré lattices. Phys. Rev. B. 2024;109:155139-155139. Google Scholar
- Song L, Liu Z, Reddy A L M, Narayanan N T, Taha-Tijerina J, Peng J, Gao G, Lou J, Vajtai R, Ajayan P M. Binary and ternary atomic layers built from carbon, boron, and nitrogen. Adv. Mater. 2012;24:4878-4878. Google Scholar
- Kim D S, Dominguez R C, Mayorga-Luna R, Ye D, Embley J, Tan T, Ni Y, Liu Z, Ford M, Gao F Y. Electrostatic moiré potential from twisted hexagonal boron nitride layers. Nat. mater. 2024;23:. Google Scholar
- Britnell L, Gorbachev R, Jalil R, Belle B, Schedin F, Mishchenko A, Georgiou T, Katsnelson M, Eaves L, Morozov S. Field-effect tunneling transistor based on vertical graphene heterostructures. Science. 2012;:335-335. Google Scholar
- Lyu B, Chen J, Wang S, Lou S, Shen P, Xie J, Qiu L, Mitchell I, Li C, Hu C. Graphene nanoribbons grown in hBN stacks for high-performance electronics. Nature. 2024;628:. Google Scholar
- Haigh S J, Gholinia A, Jalil R, Romani S, Britnell L, Elias D C, Novoselov K S, Ponomarenko L A, Geim A K, Gorbachev R. Cross-sectional imaging of individual layers and buried interfaces of graphene-based heterostructures and superlattices. Nat. Mat. 2012;11:. Google Scholar
- Sung C.-M. Graphene and hexagonal boron nitride devices. Google Patents. 2011;:. Google Scholar
- Wu Z, Liu R, Wei N, Wang L. Unexpected reduction in thermal conductivity observed in graphene/h-BN heterostructures. Phys. Chem. Chem. Phys. 2024;26:3823-3823. Google Scholar
- Chen R, Tian Y, Cao J, Ren W, Hu S, Zeng C. Unified deep learning network for enhanced accuracy in predicting thermal conductivity of bilayer graphene, hexagonal boron nitride, and their heterostructures. J. Appl. Phys. 2024;:135-135. Google Scholar
- Wang J, Mu X, Wang X, Wang N, Ma F, Liang W, Sun M. The thermal and thermoelectric properties of in-plane C-BN hybrid structures and graphene/h-BN van der Waals heterostructures. Mater. Today, Phys. 2018;5:29-29. Google Scholar
- Nguyen H T. Structural evolution of in-plane hybrid graphene/hexagonal boron nitride heterostructure upon heating. J. Mol. Graph. 2023;125:108579-108579. Google Scholar
- Kiakojouri A, Frank I, Nadimi E. Exploring the dynamics of DNA nucleotides in graphene/h-BN nanopores: insights from ab initio molecular dynamics. Phys. Chem. Chem. Phys. 2023;25:13452-13452. Google Scholar
- Stillinger F H, Weber T A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B. 1985;31:5262-5262. Google Scholar
- Bazant M Z, Kaxiras E, Justo J F. Environment-dependent interatomic potential for bulk silicon. Phys. Rev. B. 1997;56:. Google Scholar
- Justo J F, Bazant M Z, Kaxiras E, Bulatov V V, Yip S. Interatomic potential for silicon defects and disordered phases. Phys. Rev. B. 1998;58:2539-2539. Google Scholar
- Marks N. Generalizing the environment-dependent interaction potential for carbon. Phys. Rev. B. 2000;63:35401-35401. Google Scholar
- Tersoff J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B. 1988;37:6991-6991. Google Scholar
- Tersoff J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B. 1989;39:5566-5566. Google Scholar
- Nord J, Albe K, Erhart P, Nordlund K. Modeling of compound semiconductors: analytical bond-order potential for gallium, nitrogen and gallium nitride. J. Phys.: Condens. Mat. 2003;15:. Google Scholar
- Dodson B W. Development of a many-body Tersoff-type potential for silicon. Phys. Rev. B. 1987;35:2795-2795. Google Scholar
- Brenner D W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B. 1990;42:9458-9458. Google Scholar
- Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995;117:. Google Scholar
- Nguyen H T. Edge effects on the melting process of two-dimensional hexagonal boron nitride. Journal of Nanoparticle Research. 2024;26:. Google Scholar
- Nguyen H, Lieu Dan Lin, Dong Nghia Minh, Nguyen Yen Khanh. The Atomic Mechanism of the Melting Process of Free-standing Hexagonal Boron Nitride. Science and Technology Development Journal. 2024;27(4):3611-3622. Google Scholar
- Ci L, Song L, Jin C, Jariwala D, Wu D, Li Y, Srivastava A, Wang Z, Storr K, Balicas L. Atomic layers of hybridized boron nitride and graphene domains. Nature Materials. 2010;9:. Google Scholar
- Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J. Mol. Graphics. 1996;14:33-33. Google Scholar
- Lipp A, Schwetz K A, Hunold K. Hexagonal boron nitride: Fabrication, properties and applications. Journal of the European Ceramic Society. 1989;5:. Google Scholar
- Hoang V V, Tuyen L T Cam, Dong T Q. Stages of melting of graphene model in two-dimensional space. Philosophical Magazine. 2016;96:. Google Scholar
